(本小题满分13分)已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,且
,且 .若点
.若点 满足
满足 ,求
,求 的值.
的值.
(本小题满分12分)
如图,已知四棱锥P—ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,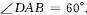 ,
,
(I)证明: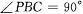 ;
;
(II)若PB =3,求直线AB与平面PBC所成角的正弦值.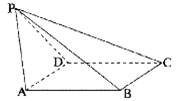
. (本小题满分12分)
已知函数
(I)求函数f(x)的单调递增区间;
(II)记ΔABC的内角A、B、C所对的边长分别为a,b,c,若 ,ΔABC的面积
,ΔABC的面积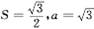 ,求b +c的值.
,求b +c的值.
.(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x-a|-2|x-1|(a∈R).
(Ⅰ)当a=3时,求函数f(x)最大值;
(Ⅱ)解关于x的不等式f(x)≥0.
(本小题满分10分)选修4-1:几何证明选讲
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=50°,求∠IEH的度数.
.(本小题满分12分)
设函数f(x)=lnx-p(x-1),p∈R.
(Ⅰ)当p=1时,求函数f(x)的单调区间;
(Ⅱ)设函数g(x)=xf(x)+p(2x2―x―1),(x≥1),求证:当p≤-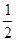 时,有g(x)≤0成立.
时,有g(x)≤0成立.