汤姆逊用来测定电子的比荷(电子的电荷量与质量之比)的实验装置如图所示,真空管内的阴极K发出的电子经加速电压加速后,穿过A'中心的小孔沿中心线O1O的方向进入到两块水平正对放置的平行极板P和P'间的区域,极板间距为d。当P和P'极板间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;当P和P'极板间加上偏转电压U后,亮点偏离到O'点;此时,在P和P'间的区域,再加上一个方向垂直于纸面向里的匀强磁场,调节磁场的强弱,当磁感应强度的大小为B时,亮点重新回到O点。不计电子的初速度、所受重力和电子间的相互作用。
(1)求电子经加速电场加速后的速度大小;
(2)若加速电压值为U0,求电子的比荷;
(3)若不知道加速电压值,但已知P和P'极板水平方向的长度为L1,它们的右端到荧光屏中心O点的水平距离为L2, O'与O点的竖直距离为h,(O'与O点水平距离可忽略不计),求电子的比荷。
一辆汽车沿一条直线向正东方向行驶,第1s内通过5m,第2s内通过20m,第3s内通过20m,第4s内通过5m.则
(1)此汽车在最初2s内的平均速度是多大?方向如何?
(2)中间2s内的平均速度是多大?全部时间内的平均速度是多大?
如图为一升降机向上做直线运动的速度﹣时间图象,根据图象求:
(1)升降机向上运动中的最大速度;
(2)升降机上升的总高度;
(3)升降机在整个上升过程中的平均速度大小.
足球以10m/s的速度水平撞击墙壁后,以8.0m/s的速度反向弹回,球与墙壁的接触时间是0.10s,则足球在这段时间内的加速度是多大?方向如何?
下表为甲乙两汽车的性能指标.开始时两车静止在同一条平直公路上,甲车在前乙车在后,两车相距170m.某时刻起两车向同一方向同时启动,若两车由静止开始运动到最大 速度的时间内都以最大加速度(启动时的加速度)做匀加速直线运动.
(1)求两车的最大加速度的大小.
(2)通过计算判断两车相遇时各做何种性质的运动?
| 启动的快慢/s(0~30m/s的加速时间) |
最大速度m•s﹣1 |
|
| 甲车 |
12 |
40 |
| 乙车 |
6 |
50 |
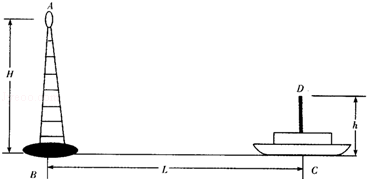
如图所示,一艘海轮用船上天线D向海岸边的信号接收器A发送电磁波脉冲信号.信号接收器和船上天线的海拔高度分别为AB=H和CD=h.船上天线某时刻发出一个电磁波脉冲信号,接收器接收到一个较强和一个较弱的脉冲,前者是直接到达的信号,后者是经海平面反射后再到达的信号,两个脉冲信号到达的时间间隔为△t,电磁波的传播速度为c,求船上天线发出此信号时海轮与海岸的距离L.