（本小题满分10分）选修4—4：坐标系与参数方程
已知曲线
的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）把的参数方程化为极坐标方程；
（2）求与交点的极坐标
．
（本题10分）设全集为R，集合A＝{x|3≤x<6}，B＝{x|2<x<9}．
（1）分别求A∩B，（∁RB）∪A；
（2）已知C＝{x|a<x<a＋1}，若C⊆B，求实数a的取值范围构成的集合．
首项都是1的两个数列{an}，{bn}（bn≠0，n∈N*）满足an＋1bn－ anbn＋1＝2bn＋1bn．
（1）令cn＝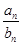
，求证：数列{cn}是等差数列；
（2）若bn＝3n－1，求数列{an}的前n项和Sn．
等差数列{an}的公差d为整数，已知a1＝10，且a4≥0，a5≤0，
（1）求{an}的通项公式；
（2）设bn＝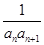
，求数列{bn}的前n项和Tn．
．三角形ABC中，内角A、B、C的对边分别为a、b、c，若a、b是方程x2－2
x＋2＝0的两根，且2cos（A＋B）＝1．
（1）求角C的度数；
（2）求c；
（3）求△ABC的面积．
等差数列
满足
，
．
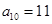（Ⅰ）求的通项公式；
（Ⅱ）令
求
的最大项和最小项的值．