如图所示,已知AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )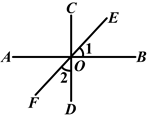
| A.相等 |
| B.互余 |
| C.互补 |
| D.互为对顶角 |
勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )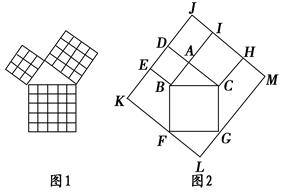
| A.90 | B.100 | C.110 | D.121 |
如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则b的面积为( )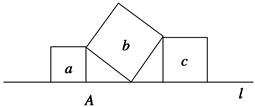
| A.4 | B.6 | C.16 | D.55 |
如图,将等腰直角三角形沿虚线剪去顶角后,∠1+∠2=( )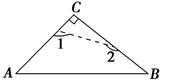
| A.225° | B.235° |
| C.270° | D.与虚线的位置有关 |
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.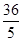 |
B.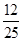 |
C.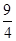 |
D.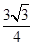 |
如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是 ( )
| A.20 | B.10 | C.5 | D.52 |