某校高三一次月考之后,为了了解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成下面频率分布表:
(1)若每组数据用该区间的中点值(例如区间[90,100 )的中点值是95)作为代表,试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在区间[110,130 )中的学生数为ξ,求:
①在三次抽取过程中至少两次连续抽中成绩在区间[110,130 )中的概率;
②ξ的分布列和数学期望.
(本小题满分12分)已知函数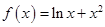 .
.
(1)若函数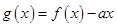 在定义域内为增函数,求实数
在定义域内为增函数,求实数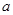 的取值范围;
的取值范围;
(2)在(1)的条件下,若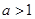 ,
,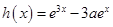 ,
,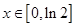 ,求
,求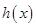 的极小值;
的极小值;
(3)设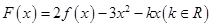 ,若函数
,若函数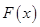 存在两个零点
存在两个零点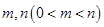 ,且满足
,且满足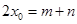 ,问:函数
,问:函数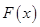 在点
在点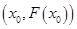 处的切线能否平行于
处的切线能否平行于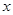 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
(本小题满分12分)已知函数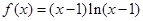 .
.
(1)设函数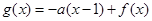 在区间
在区间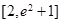 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(2)若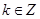 ,且
,且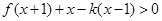 对
对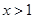 恒成立,求
恒成立,求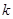 的最大值.
的最大值.
(本小题满分12分)如图,在等腰直角三角形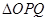 中,
中,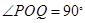 ,
,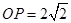 ,点
,点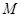 在线段
在线段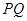 上.
上.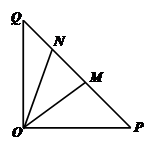
(1)若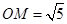 ,求
,求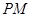 的长;
的长;
(2)若点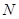 在线段
在线段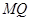 上,且
上,且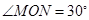 ,问:当
,问:当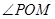 取何值时,
取何值时,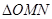 的面积最小?并求出面积的最小值.
的面积最小?并求出面积的最小值.
(本小题满分12分)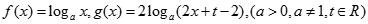 .
.
(1)当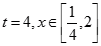 时,
时,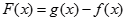 的最小值是
的最小值是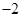 ,求
,求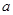 的值;
的值;
(2)当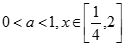 时,有
时,有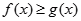 恒成立,求实数
恒成立,求实数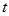 的取值范围.
的取值范围.
(本小题满分12分)已知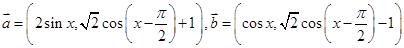 ,设
,设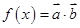 .
.
(1)求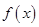 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)在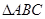 中,
中,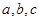 分别为
分别为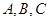 的对边,且
的对边,且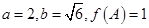 ,求边
,求边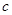 .
.