(本小题满分12分)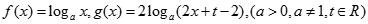 .
.
(1)当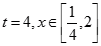 时,
时,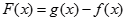 的最小值是
的最小值是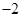 ,求
,求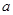 的值;
的值;
(2)当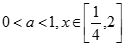 时,有
时,有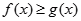 恒成立,求实数
恒成立,求实数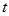 的取值范围.
的取值范围.
设数列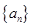 的前
的前 项和为
项和为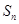 ,点
,点 在直线
在直线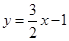 上.
上.
(1)求数列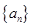 的通项公式;
的通项公式;
(2)在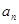 与
与 之间插入
之间插入 个数,使这
个数,使这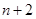 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
如图,菱形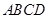 的边长为4,
的边长为4,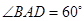 ,
,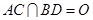 .将菱形
.将菱形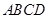 沿
沿
对角线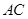 折起,得到三棱锥
折起,得到三棱锥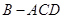 ,点
,点 是棱
是棱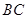 的中点,
的中点,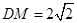 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC
(3)求三棱锥B﹣DOM的体积.
已知直线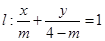
(1)若直线 的斜率等于2,求实数
的斜率等于2,求实数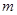 的值;
的值;
(2)若直线 分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
(本小题满分14分)已知函数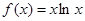 ,
,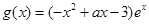 (a为实数).
(a为实数).
(1) 当a=5时,求函数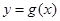 在
在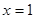 处的切线方程;
处的切线方程;
(2) 求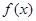 在区间[t,t+2](t >0)上的最小值;
在区间[t,t+2](t >0)上的最小值;
(Ⅲ) 若存在两不等实根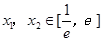 ,使方程
,使方程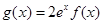 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(本小题满分13分) 已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为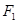 和
和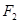 ,且|
,且|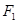
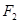 |=2,点(1,
|=2,点(1,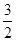 )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过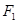 的直线
的直线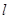 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若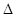 A
A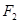 B的面积为
B的面积为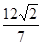 ,求以
,求以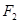 为圆心且与直线
为圆心且与直线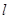 相切圆的方程.
相切圆的方程.