已知函数 在
在 处取得极值.
处取得极值.
(1)确定a的值;
(2)若 ,讨论g(x)的单调性.
,讨论g(x)的单调性.
某渔业公司今年初用98万元购进一艘渔船用于捕捞,第一 年需各种费用12万
年需各种费用12万
元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的
总收入为50万元.
(1)该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)?
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
某企业 甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
(1)写出销量q与售价p的函数关系式;
(2)当售价p定为多少时,月利润最多?
(3)企业乙最早可望在经营该专卖店几个月后还清转让费?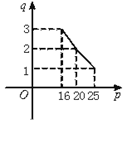
设f(x)是定义在[-1,1]上的奇函数,且对任意的实数a,b∈[-1,1],当a+b
≠0时,都有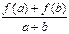 >0.
>0.
(1)若a>b,试比较f(a)与f(b)的大小;
(2)解不等式f(x -
- )<f(x-
)<f(x-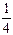 );
);
(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集是空集,求c的取值范围.
已知函数f(x)=loga[(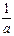 -2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
-2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
记关于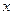 的不等式
的不等式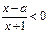 的解集为
的解集为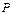 ,不等式
,不等式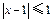 的解集为
的解集为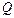 .
.
(1)若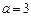 ,求集合
,求集合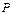 ;
;
(2)若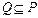 ,求正数
,求正数 的取值
的取值 范围.
范围.