甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的数学期望.
(本小题满分12分)
某大学对参加了“世博会”的该校志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大 学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为
学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为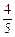 、
、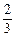 、
、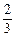 ,他们考核所得的等次相互独立。
,他们考核所得的等次相互独立。
(Ⅰ)求在这次考核中,志愿者甲、乙、两三人中至少有一名考核为优秀的概率;
(Ⅱ)记这这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量x,求随机变量x的分布列和数学期望Ex。
(本小题满分10分)
在 中,
中, 、
、 、
、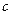 分别为角A、B、C的对边,且
分别为角A、B、C的对边,且 ,
, ,(其中
,(其中 ).
).
(Ⅰ)若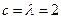 时,求
时,求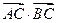 的值;
的值;
(Ⅱ)若 时,求边长
时,求边长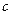 的最小值及判定此时
的最小值及判定此时 的形状。
的形状。
、设函数f(x) = x2+bln(x+1),
(1)若对定义域的任意x,都有f(x)≥f(1)成立,求实数b的值;
(2)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(3)若b=-1,证明对任意的正整数n,不等式 成立;
成立;
(12 分)已知椭圆
分)已知椭圆 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且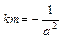 .
.
(Ⅰ)求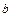 的值;
的值;
(Ⅱ)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈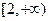 ,使得四边形OACB是平行四边形,请证明你
,使得四边形OACB是平行四边形,请证明你 的结论;
的结论;
已知四棱锥 中,
中, 平面
平面 ,底面
,底面
 是直角梯形,
是直角梯形,
 为
为
 的重心,
的重心, 为
为 的中点,
的中点, 在
在 上,且
上,且 ;
;
(1)求证: ;
;
(2)当
 二面角
二面角 的正切值为多少时,
的正切值为多少时, 平面
平面 ;
;
(3)在(2)的条件下,求直线 与平面
与平面 所
所 成角
成角
的正弦值;