如图所示,一带电荷量为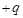 、质最为m的小物块处于一倾角为37°的光滑斜面上,当整个装置置于一水平向右的匀强电场中,小物块恰好静止。已知重力加速度为g,
、质最为m的小物块处于一倾角为37°的光滑斜面上,当整个装置置于一水平向右的匀强电场中,小物块恰好静止。已知重力加速度为g, 。
。
(1)求水平向右匀强电场的电场强度大小;
(2)若将电场强度减小为原来的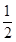 ,求电场强度变化后物块沿斜面下滑距离L时的动能。
,求电场强度变化后物块沿斜面下滑距离L时的动能。
如右图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°。一质量为m,带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场。已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中的磁感应强度的大小。(忽略粒子重力)。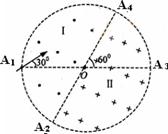
如图所示,ABC是一条由一个半圆和一段斜面组成的光滑轨道,半圆轨道与轨道BC在同一竖直平面内且在B点平滑连接。A、B两点在同一竖直线上,且已知半圆半径为R。今在水平地面上某一点P处抛出一个小球,使它恰好从A点相切进入轨道(此过程不相碰),在B点处无能量损失,最后沿斜面上升到高度为H处。试求小球抛出点P点的位置,抛射速度Vp以及抛射角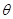 (不计空气阻力)。
(不计空气阻力)。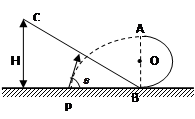
太阳内部四个质子聚变成一个粒子,同时发射两个正电子和两个没有静止质量的中微子。若太阳辐射能量的总功率P,质子、氦核、正电子的质量分别为mp、mHe、me,真空中光速为c。求t时间内参与核反应的质子数。
如图所示,在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体OPQ,OP=OQ=R,一束单色光垂直OP面射入玻璃体,在OP面上的入射点为A,OA=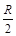 ,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD=
,此单色光通过玻璃体后沿BD方向射出,且与x轴交于D点,OD=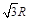 ,求:该玻璃的折射率是多少?
,求:该玻璃的折射率是多少?
如图,竖直平面内有一直角形内径相同的细玻璃管,A端封闭,C端开口,AB=BC= ,且此时A、C端等高。平街时,管内水银总长度为
,且此时A、C端等高。平街时,管内水银总长度为 ,玻璃管AB内封闭有长为
,玻璃管AB内封闭有长为 的空气柱。已知大气压强为
的空气柱。已知大气压强为 汞柱高。如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体的压强为多少汞柱高?管内封入的气体可视为理想气体且温度不变。
汞柱高。如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体的压强为多少汞柱高?管内封入的气体可视为理想气体且温度不变。