如图所示, ,两物体与地面间的动摩擦因数均为0.2,当大小为F=5N水平拉力作用在物体A上时,求物体A的加速度。(忽略滑轮的质量以及滑轮和绳的,取
,两物体与地面间的动摩擦因数均为0.2,当大小为F=5N水平拉力作用在物体A上时,求物体A的加速度。(忽略滑轮的质量以及滑轮和绳的,取 )
)
(14分)羚羊从静止开始奔跑,经过50m的距离能加速到最大速度25m/s,并能维持一段较长时间,猎豹从静止开始奔跑,经过60m的距离能加速到最大速度30m/s,以后只能维持这个速度4.0s,设猎豹距离羚羊x米时开始攻击,羚羊则从猎豹1.0s后开始奔跑,假设羚羊和猎豹在加速阶段分别做匀加速运动,且沿同一直线,求
(1)猎豹要在最大速度减速前追上羚羊,x应在什么范围内取值?
(2)猎豹要在加速阶段追上羚羊,x应在什么范围内取值?
(12分)如图甲所示,水平传送带AB的长度L=3.75m,皮带轮的半径R=0.1m。现有一小物体(视为质点)以水平速度v0从A点滑上传送带,物块与传送带间动摩擦因数为μ=0.2,传送带上表面距地面的高度h=5m, g取10m/s2,试讨论下列问题: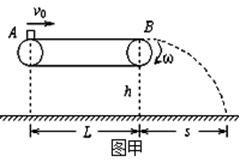
(1)若皮带静止,要使小物体滑到B端后做平抛运动.则小物体滑上A点的初速度v0至少为多少?
(2)若皮带轮以角速度 =40rad/s顺时针匀速转动,小物体滑上A点的初速度v0="3" m/s,求小物体由A点运动到B点的时间及落地点到B的水平位移s;
=40rad/s顺时针匀速转动,小物体滑上A点的初速度v0="3" m/s,求小物体由A点运动到B点的时间及落地点到B的水平位移s;
(3)若皮带轮以角速度 =40rad/s顺时针匀速转动,求v0满足什么条件时,小物块均落到地面上的同一点.
=40rad/s顺时针匀速转动,求v0满足什么条件时,小物块均落到地面上的同一点.
如图所示,在水平转台的光滑水平横杆上穿有两个质量分别为2m和m的小球A和B,A、B间用劲度系数为k的轻质弹簧连接,弹簧的自然长度为L,当转台以角速度ω绕竖直轴匀速转动时,如果A、B仍能相对横杆静止而不碰左右两壁,求: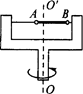
(1)A、B两球分别离开中心转轴的距离.
(2)若转台的半径也为L,求角速度ω的取值范围.
(9分)如图所示,底座A上装有长0.5m的直立杆,总质量为1kg,用细线悬挂,底座底面离水平地面H=0.2m,杆上套有质量为0.2kg的小环B,它与杆间有摩擦,设环与杆相对滑动时摩擦力大小始终不变,环从底座以 m/s的初速度沿杆向上运动,最后恰能到达杆的顶端(取g=10m/s2)。求:
m/s的初速度沿杆向上运动,最后恰能到达杆的顶端(取g=10m/s2)。求:
⑴环沿杆上滑过程中的加速度大小;
⑵在环上滑过程中,细线对杆的拉力大小;
⑶若小环在杆顶端时细线突然断掉,底座下落后与地面立即粘合后静止,整个过程杆没有晃动,则线断后经多长时间环第一次与底座相碰?
如图所示,一小球自平台上水平抛出,恰好落在临近平台的一倾角为α=53°的斜面顶端,并刚好沿斜面下滑,已知斜面顶端与平台的高度差h=0.8 m,g=10 m/s2,sin 53°=0.8,cos 53°=0.6,则:
(1)小球水平抛出的初速度v0是多少?
(2)斜面顶端与平台边缘的水平距离s是多少?
⑶小球与斜面的动摩擦因数μ=0.5,斜面高H=16m,小球到达斜面底端的速度多大?