如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.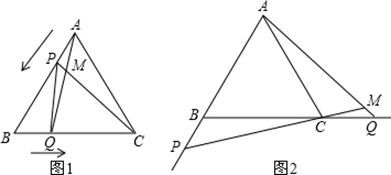
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
(本小题满分6分)解分式方程:
(本小题满分6分)先化简,再求值: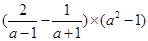 ,其中
,其中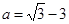
已知直线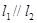 ,直线
,直线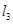 与
与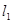 、
、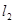 分别交于
分别交于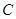 、
、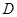 两点,点
两点,点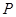 是直线
是直线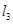 上的一动点
上的一动点
(1)如图①,若动点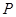 在线段
在线段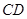 之间运动(不与
之间运动(不与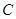 、
、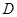 两点重合),问在点
两点重合),问在点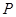 的运动过程中是否始终具有
的运动过程中是否始终具有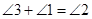 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图②,当动点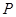 在线段
在线段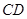 之外且在的上方运动(不与
之外且在的上方运动(不与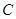 、
、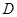 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;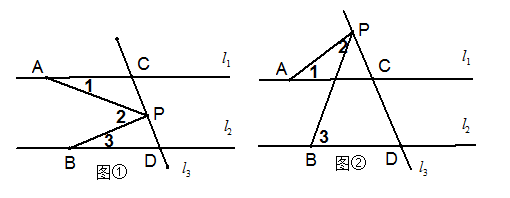
某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
| 数量范围(千克) |
0~500 |
500以上~1500 |
1500以上~2500 |
2500以上 |
| 价格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需要 元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。
出租车司机小李某天下午营运全是在东西走向的人民大道进行的,如果规定向东为正,向西为负,他这天下午行车里程如下:
+15,-3,+14,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少千米?
(2)若每千米耗油4升,这天下午共耗油多少升?