九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识,在三张完全相同且不透明的卡片正面分别写上了 ,0,2三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为 ,再从剩下的两张中随机取出一张,将卡片上的数字记为 ,然后叫万宇在平面直角坐标系中找出点 的位置.
(1)请你用树状图帮万宇同学进行分析,并写出点 所有可能的坐标;
(2)求点 在第二象限的概率;
(3)张老师在万宇同学所画的平面直角坐标系中,画了一个半径为3的 ,过点 能作多少条 的切线?请直接写出答案.
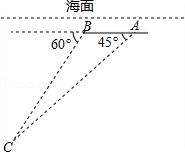
如图,埃航 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的 点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达 点,在 处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子 点距离海面的深度(结果保留根号).
已知:如图 三个顶点的坐标分别为 、 、 ,正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出 向上平移6个单位得到的△ ;
(2)以点 为位似中心,在网格中画出△ ,使△ 与 位似,且△ 与 的位似比为 ,并直接写出点 的坐标.

如图,在平面直角坐标系中,点 为坐标原点,直线 与抛物线 相交于 , , 两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点 ,使得 是以线段 为斜边的直角三角形?若存在,求出点 的坐标;若不存在,说明理由;
(3)点 是线段 上一动点,(点 不与点 、 重合),过点 作 ,交第一象限内的抛物线于点 ,过点 作 轴于点 ,交 于点 ,若 、 的面积 、 满足 ,求出 的值,并求出此时点 的坐标.

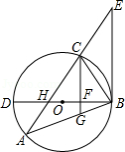
如图, 内接于 , 为 的直径, 与 相交于点 , 的延长线与过点 的直线相交于点 ,且 .
(1)求证: 是 的切线;
(2)已知 ,且 与 、 分别相交于点 、 ,若 , , ,求 的值.