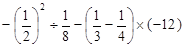已知如图平面直角坐标系中，点O是坐标原点，矩形ABCO是顶点坐标分别为A（3，0）、B（3，4）、C（0，4）．点D在y轴上，且点D的坐标为（0，﹣5），点P是直线AC上的一动点．
（1）当点P运动到线段AC的中点时，求直线DP的解析式（关系式）；
（2）当点P沿直线AC移动时，过点D、P的直线与x轴交于点M．问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M？若存在，请求出点M的坐标；若不存在，请说明理由；
（3）当点P沿直线AC移动时，以点P为圆心、R（R＞0）为半径长画圆．得到的圆称为动圆P．若设动圆P的半径长为
，过点D作动圆P的两条切线与动圆P分别相切于点E、F．请探求在动圆P中是否存在面积最小的四边形DEPF？若存在，请求出最小面积S的值；若不存在，请说明理由．
如图，直线AB与CD相交于点O，∠AOC=50°，OE平分∠AOD，OF平分∠BOD.
（1）填空：∠BOD=度；
（2）试说明OE⊥OF.
如图，在方格纸中，我们把每个小正方形的顶点称为格点，已知点A、B、C都在格点上，且每个小正方形的边长都为1.
（1）画线段AB，并过点C作CD⊥AB，垂足为点D；
（2）连结AC、BC.
①求△ABC的面积；
②已知AB=5，求(1)中线段CD的长.
如图，已知BD∥CE.
（1）若∠C=70°，则∠DBC=______°；
（2）若∠C=∠D，则AC∥DF.
请阅读下面的说理过程，并填写适当的理由或数学式.
解：∵BD∥CE(已知)，
∴∠1=∠C()，
又∵∠C=∠D(已知)，
∴∠1=(等量代换)，
∴AC∥DF().
先化简，再求值：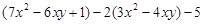
，其中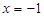
，
.
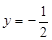计算：