如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B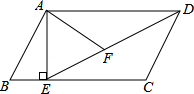
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6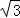 ,AF=4
,AF=4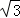 ,求AE的长.
,求AE的长.
计算:
如图,抛物线 过点 ,且与直线 交于 、 两点,点 的坐标为 .

(1)求抛物线的解析式;
(2)点 为抛物线上位于直线 上方的一点,过点 作 轴交直线 于点 ,点 为对称轴上一动点,当线段 的长度最大时,求 的最小值;
(3)设点 为抛物线的顶点,在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.
在矩形 中,连结 ,点 从点 出发,以每秒1个单位的速度沿着 的路径运动,运动时间为 (秒 .过点 作 于点 ,在矩形 的内部作正方形 .
(1)如图,当 时,
①若点 在 的内部,连结 、 ,求证: ;
②当 时,设正方形 与 的重叠部分面积为 ,求 与 的函数关系式;
(2)当 , 时,若直线 将矩形 的面积分成 两部分,求 的值.

如图,南海某海域有两艘外国渔船 、 在小岛 的正南方向同一处捕鱼.一段时间后,渔船 沿北偏东 的方向航行至小岛 的正东方向20海里处.
(1)求渔船 航行的距离;
(2)此时,在 处巡逻的中国渔政船同时发现了这两艘渔船,其中 渔船在点 的南偏西 方向, 渔船在点 的西南方向,我渔政船要求这两艘渔船迅速离开中国海域.请分别求出中国渔政船此时到这两艘外国渔船的距离.(注 结果保留根号)

如图,直线 与双曲线 相交于点 ,且 ,将直线向左平移一个单位后与双曲线相交于点 ,与 轴、 轴分别交于 、 两点.
(1)求直线 的解析式及 的值;
(2)连结 、 ,求 的面积.
