(本小题满分13分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
.(本小题满分14分)
已知数列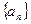 满足
满足 且
且
(1)求 ;
;
(2)数列 满足
满足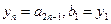 ,且
,且 时
时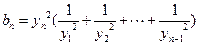 .
.
证明当 时,
时, 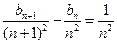 ;
;
(3)在(2)的条件下,试比较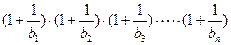 与4的大小关系.
与4的大小关系.
. (本小题满分13分)
设A ,B
,B 是椭圆
是椭圆 上的两点,
上的两点, 为坐标原点,向量
为坐标原点,向量 ,向量
,向量 。
。
(1)设 ,证明:点M在椭圆上;
,证明:点M在椭圆上;
(2)若点P、Q为椭圆上两点,且 ∥
∥ 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
(本小题满分12分)
已知函数 .
.
(1)求a的取值范围;
(2)若对任意的 成立,求
成立,求 的取值范围。
的取值范围。
. (本小题满分12分)
如图,四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,已知AB=
 ,∠APB=∠ADB=60°
,∠APB=∠ADB=60°
(Ⅰ)证明:平面PAC⊥平面PBD;
(Ⅱ)求PH与平面PAD所成的角的大小.
(本小题满分12分)
某电视台为了宣传某沿江城市经济崛起的情况,特举办了一期有奖知识问答活动,活动对18—48岁的人群随机抽取n人回答问题“沿江城市带包括哪几个城市”,统计数据结果如下表:
| 组数 |
分组 |
回答正 确的人数 |
占本组 的频率 |
| 第1组 |
[18,28〕 |
240 |
X |
| 第2组 |
[28,38〕 |
300 |
0.6 |
| 第3组 |
[38,48〕 |
a |
0.4 |

(Ⅰ)分别求出n,a,x的值;
(Ⅱ)若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48〕内回答正确的得奖金200元,年龄在[18,28〕内回答正确的得奖金100元。主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答正确,求该家庭获得奖金 的分布列及数学期望(两人回答问题正确与否相互独立)。
的分布列及数学期望(两人回答问题正确与否相互独立)。