(本小题满分12分)如图,在四棱锥中,底面是正方形,底面,, 点 分别是
分别是 的中点,,且交于点.
的中点,,且交于点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面⊥平面;
已知函数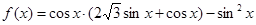 .
.
(Ⅰ)求函数 在区间
在区间 上的最大值及相应的
上的最大值及相应的 的值;
的值;
(Ⅱ)若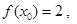 且
且 ,求
,求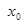 的值.
的值.
(本题12分)在 中,
中, 、
、 、
、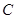 的对边分别为
的对边分别为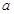 、
、 、
、 ,已知
,已知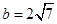 ,
,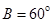 ,
,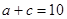 .
.
(1)求 ;
;
(2)若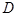 为
为 外接圆劣弧AC上的一点,且
外接圆劣弧AC上的一点,且 ,求四边形
,求四边形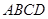 的面积.
的面积.
(本题12分) 我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是6万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度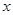 (厘米)满足关系式:
(厘米)满足关系式: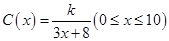 ,若无隔热层,则每年能源消耗费用为5万元.设
,若无隔热层,则每年能源消耗费用为5万元.设 为隔热层建造费用与使用20年的能源消耗费用之和.
为隔热层建造费用与使用20年的能源消耗费用之和.
(1)求C(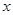 )和
)和 的表达式;
的表达式;
(2)当陋热层修建多少厘米厚时,总费用 最小,并求出最小值.
最小,并求出最小值.
(本题12分)已知函数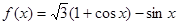 ,在
,在 中,
中,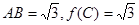 ,且
,且 的面积为
的面积为 .
.
(1)求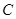 的值;(2)求
的值;(2)求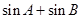 的值.
的值.
(本题12分)已知:等差数列{ }中,
}中, =14,前10项和
=14,前10项和 .
.
(1)求 ;
;
(2)将{ }中的第2项,第4项, ,第
}中的第2项,第4项, ,第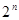 项按原来的顺序排成一个新数列{
项按原来的顺序排成一个新数列{ },求数列{
},求数列{ }的前
}的前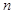 项和
项和 .
.