在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) |
300 |
500 |
| 概率 |
0.5 |
0.6 |
| 作物市场价格(元/kg) |
6 |
10 |
| 概率 |
0.4 |
0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
(1)求证:AB∥GH;
(2)求平面PAB与平面PCD所成角的正弦值.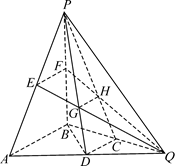
已知数列 的前
的前 项和为
项和为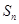 ,
,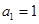 ,
, ,
, ,其中
,其中 为常数.
为常数.
(1)证明: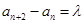 ;
;
(2)当 为何值时,数列
为何值时,数列 为等差数列?并说明理由.
为等差数列?并说明理由.
已知函数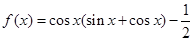 .
.
(1)若 ,且
,且 ,求
,求 的值;
的值;
(2)当 取得最小值时,求自变量
取得最小值时,求自变量 的集合.
的集合.
已知函数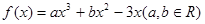 ,在点
,在点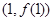 处的切线方程为
处的切线方程为 .
.
(I)求函数 的解析式;
的解析式;
(II)若对于区间 上任意两个自变量的值
上任意两个自变量的值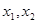 ,都有
,都有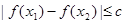 ,求实数
,求实数 的最小值;
的最小值;
(III)若过点 ,可作曲线
,可作曲线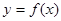 的三条切线,求实数
的三条切线,求实数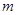 的取值范围.
的取值范围.