(本小题满分10分)已知箱中装有2个白球,3个黑球,每次从中任取一球(不放回),取完白球则停止取球.
(1)求取2次后仍不能停止的概率;
(2)记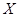 为停止取球后取球的次数,求
为停止取球后取球的次数,求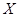 的数学期望
的数学期望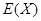 .
.
(满分8分)已知
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
已知函数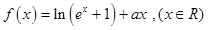 是偶函数,且在区间
是偶函数,且在区间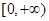 上是增函数,
上是增函数,
(1)试确定实数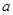 的值;
的值;
(2)先判断函数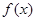 在区间
在区间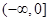 上的单调性,并用定义证明你的结论;
上的单调性,并用定义证明你的结论;
(3)关于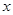 的不等式
的不等式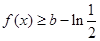 在
在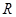 上恒成立,求实数
上恒成立,求实数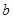 的取值范围。
的取值范围。
为节约用水,某市打算出台一项水费收费措施,其中规定:每月每户用水量不超过7吨时,每吨水费收基本价3元;若超过7吨而不超过11吨时,超过部分水费加收100%;若超过11吨而不超过15吨时,超过部分的水费加收200%, , 现在设某户本月实际用水量为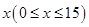 吨,应交水费为
吨,应交水费为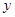 元.
元.
(1)试求出函数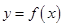 的解析式;
的解析式;
(2)如果一户人家本月应交水费为39元,那么该户本月的实际用水量是多少?
如图所示,矩形ABDE中,AB=3,BD=6,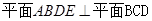 ,又在
,又在 中,点F为BC的中点,且
中,点F为BC的中点,且
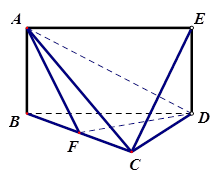
(1)求证: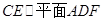 ;
;
(2)求证: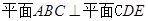 ;
;
(3)求三棱锥A—CDE的体积V。
(1)在所给的平面直角坐标系内, 画出函数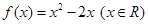 的图象, 并根据图象写出函数
的图象, 并根据图象写出函数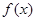 的单调区间(不要求证明);
的单调区间(不要求证明);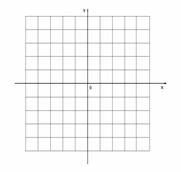
(2)求函数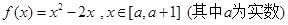 的最小值。
的最小值。