已知 是方程
是方程 的一个根,求
的一个根,求 的值及方程的另一个根.
的值及方程的另一个根.
(1)x(x+4)=-5(x+4);(2)
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)问加工成的正方形零件的边长是多少mm?
小颖善于反思,她又提出了如下的问题.
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请计算.
如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.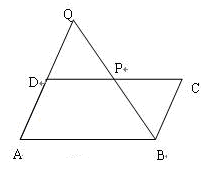
(1)求证:△AQB∽△CBP;
(2)当AB=2PC时,,求证:点D为AQ的中点.
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?