某房地产开发公司用2.56×107元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房,经测算,如果将楼房建为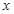 (
(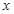 ≥10)层,则每平米的平均建筑费用为1000+50
≥10)层,则每平米的平均建筑费用为1000+50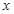 (单位:元)
(单位:元)
(Ⅰ)写出楼房平均综合费用y关于建造层数x的函数关系式;
(Ⅱ)该楼房应建造多少层时,可使楼房每平米的平均综合费用最少?最少费用是多少?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
已知直线l经过直线3x+4y﹣2=0与直线2x+3y﹣2=0的交点 ,且垂直于直线x﹣2y﹣1=0.
,且垂直于直线x﹣2y﹣1=0.
(Ⅰ)求直线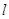 的方程;
的方程;
(Ⅱ)求直线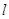 与两坐标轴围成的三角形的面积S.
与两坐标轴围成的三角形的面积S.
在△ABC中,角A,B,C的对边分别是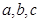 且
且 .
.
(1)求角B的大小;
(2)若 =4,
=4,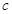 =3,D为BC的中点,求△ABC的面积及AD的长度.
=3,D为BC的中点,求△ABC的面积及AD的长度.
求圆心在直线2x﹣y﹣3=0上,且过点A(5,2)和点B(3,2)的圆的方程.
数列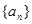 的前
的前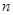 项和为
项和为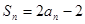 ,
,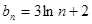 ,函数
,函数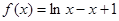 .
.
(1)求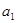 的值和数列
的值和数列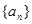 的通项公式;
的通项公式;
(2)证明:当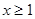 时,
时,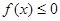 ;
;
(3)求证: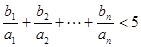 .
.