(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
 |
 |
 |
 |
加工的时间 (小时) (小时) |
 |
 |
 |
 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出 关于
关于 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工 个零件需要多少时间?
个零件需要多少时间?
己知下列三个方程: x2+4ax-4a+3="0," x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,求实数a的取值范围.
(本题满分12分)如图,正四棱柱ABCD—A1B1C1D1中,底面边长为 ,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
(1)求证:B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1—EFD1的体积V.
(本题满分12分)四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,且侧面PAD与底面ABCD垂直,E为PD的中点。
(1) 求证:PB//面ACE;
(2) 求二面角E—AC—D的大小。
(本题满分12分)在某次射击比赛中共有5名选手,出场时甲、乙、丙三人不能相邻。求(1)共有多少种不同的出场顺序?
(2)若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
(3)若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5,求三人各射击一
次至少有两人命中目标的概率。
(本题满分13分)在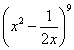 展开式中,求:
展开式中,求:
(1)第6项;(2) 第3项的系数;(3)常数项。