2015年元旦联欢晚会某师生一块做游戏,数学老师制作了六张卡片放在盒子里,卡片上分别写着六个函数:分别写着六个函数: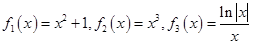 ,
,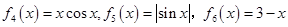 .
.
(1)现在取两张卡片,记事件A为“所得两个函数的奇偶性相同”,求事件A的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是奇函数则停止抽取,否则继续进行,记停止时抽取次数为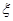 ,写出
,写出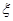 的分布列,并求其数学期望.
的分布列,并求其数学期望.
(本小题满分12分)
四 棱锥
棱锥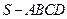 的底面
的底面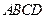 是
是 正方形,侧棱
正方形,侧棱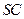 的中点
的中点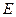 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形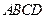 的中心
的中心 ,
, 顶点
顶点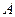 在截面
在截面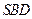 内
内 的射影恰好是
的射影恰好是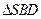 的重心
的重心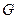 .
.
(1)求直线 与底面
与底面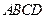 所成角的正切值;
所成角的正切值;
(2)设 ,求此四棱锥过点
,求此四棱锥过点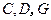 的截面面积.
的截面面积.
(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样, 购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为
购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求三位同学都没有中奖的概率;


(Ⅱ)求三位同学中至少有两位没有中 奖的概率.
奖的概率.
(本小题满 分10分)
分10分)
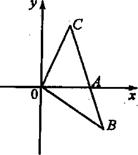
如图,在平面直角坐标系中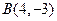 ,点
,点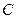 在第一象限内,
在第一象限内,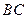 交
交 轴于点
轴于点 ,
, .
.
(1)求 的长;
的长;
(2)记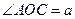 ,
,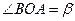 .(
.(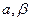 为锐角),求sina,sin
为锐角),求sina,sin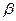 的值
的值
((本小题满分12分)
中心在原点,焦点在x轴上的椭圆,率心率 ,此椭圆与直线
,此椭圆与直线 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).
(1)求椭圆方程;
(2)若M是椭圆上任意一点, 、
、 为椭圆的两个焦点,求
为椭圆的两个焦点,求 的取值范围;
的取值范围;
(
(本小题满分12分)
已知 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.