（本小题满分14分）已知函数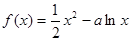
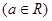
（1）求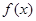
的单调区间和极值；
（2）设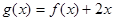
，若
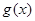在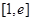
上不单调且仅在
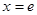处取得最大值，求
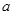的取值范围；
（3）当
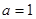时，探究当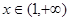
时，函数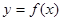
的图像与函数
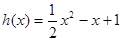图像之间的关系，并证明你的结论．
△ABC的内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB。
（1）求B；
（2）若b=2，求△ABC面积的最大值。
△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB．
（1）求B；
（2）若b=2，求△ABC面积的最大值。
设△ABC的内角A，B，C所对的边分别为a，b，c，(a+b+c)(a－b+c)=ac
(1)求B
(2)若sinAsin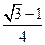C=
，求C
已知椭圆
的离心率
，连接椭圆的四个顶点得到的菱形的面积为4．
(1)求椭圆的方程；
(2)设直线
与椭圆相交于不同的两点
，已知点
的坐标为
，点
在线段
的垂直平分线上，且
，求
的值.
已知椭圆G：
．过点(m，0)作圆
的切线l交椭圆G于A，B两点．
(1)求椭圆G的焦点坐标和离心率；
(2)将
表示为m的函数，并求的最大值．