如图所示，一足够长的平直木板C静止在光滑水平面上，现有两小物块A和B分别以2v0和v0的水平初速度从长木板C两端滑上长木板。已知物块A、B与长木板C间的动摩擦因数均为
，A、B、C三者质量相等，重力加速度为g。求：
（1）A、B刚滑上C时，A、B、C的加速度大小；
（2）物块B相对于木板C静止时，A的速度大小；
（3）物块A、B开始滑上C到A、B都静止在C上为止，经历的时间以及B通过的位移。
甲、乙两车在同一车道上同向行驶，速度都是30 m/s，甲在前乙在后。某时甲突然以2.0 m/s2的加速度减速刹车，乙看到情况后，过1.0 s才开始刹车，乙刹车的加速度为2.2 m/s2，要避免追尾事故，甲、乙两车原来至少要相距多少？
如图所示，两个完全相同的球，重力大小均为G ，两球与水平地面间的动摩擦因数都为μ，且假设最大静摩擦力等于滑动摩擦力，一根轻绳两端固结在两个球上，在绳的中点施加一个竖直向上的拉力，当绳被拉直后，两段绳间的夹角为α.问当F至少为多大时，两球将会发生滑动？
一辆汽车性能的优劣，其油耗标准非常重要，而影响汽车油耗标准最主要的因素是其在行进中所受到的空气阻力．人们发现汽车在高速行驶中所受到的空气阻力Ff(也称风阻)主要与两个因素有关．一是汽车正面投影面积S；二是汽车行驶速度
.
某研究人员在汽车风洞实验室中通过模拟实验得到下列所列数据：
（1）请写出由上述数据得出的汽车风阻Ff与汽车正面投影面积S及汽车行驶的速度的关系式(可以用k表示比例系数)．
(2) 请由上述数据求出比例系数k的大小和单位．
如图所示，质量为20kg的方形物体置于水平面上，它与水平面之间的动摩擦因数为μ，两等长轻弹簧OA、OB一端分别连接于物体上相距为24cm的A、B两点，另一端共同连结于O点。当两轻弹簧刚好处于自由状态时，它们构成了一个1060的张角。现用一垂直于AB连线的水平力F向右拉O点，当把两弹簧之间的张角拉成740时，物体恰好能在水平面上匀速前进，此时两弹簧还等长。求动摩擦因数μ的大小。(已知弹簧的劲度系数为k =1000N/m sin370=0.6 g=10m/s2 )
如图所示， \倾角为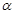
的斜面体（斜面光滑且足够长）固定在水平地面上，斜面顶端与劲度系数为
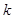、自然长度为
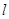的轻质弹簧相连，弹簧的另一端连接着质量为
的物块。压缩弹簧使其长度为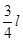
时将物块由静止开始释放（物快做简谐运动），且物块在以后的运动中，斜面体始终处于静止状态。重力加速度为
。
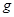（1）求物块处于平衡位置时弹簧的长度；
（2）物块做简谐运动的振幅是多少；
（3）选物块的平衡位置为坐标原点，沿斜面向下为正方向建立坐标轴，用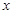
表示物块相对于平衡位置的位移，证明物块做简谐运动；（已知做简谐运动的物体所受的恢复力满足 F=—kx）