（本小题12分）2014年2月，西非开始爆发埃博拉病毒疫情，埃博拉病毒是引起人类和灵长类动物发生埃博拉出血热的烈性病毒，引发了世界恐慌。中国国际救援组织立即采用分层抽样的方法从病毒专家、心理专家、地质专家三类专家中抽取若干人组成研究团队赴西非工作，有关数据见表1（单位：人）.
病毒专家为了检测当地群众发烧与是否更易受博拉病毒疫情影响，在当地随机选取了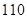
群众进行了检测，并将有关数据整理为不完整的
列联表（表2）.
表1：
| |
相关人员数 |
抽取人数 |
| 病毒专家 |
48 |
 |
| 心理专家 |
24 |
 |
| 地质专家 |
72 |
6 |
表2：
| |
发烧 |
无发烧 |
合计 |
| 患Ebola |
50 |
 |
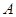60 |
| 不患Ebola |
 |
40 |
50 |
| 合计 |
 |
 |
 |
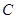（1）求
；
（2）写出表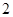
中
的值，并判断是否有99.9%的把握认为疫情地区的群众发烧与患Ebola病毒有关；
（3）若从研究团队的病毒专家和心理专家中随机选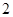人撰写研究报告，求其中恰好有
人为病毒专家的概率.
临界值表：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
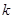2.072 |
2.706 |
3.841 |
5.024 |
6. 635 |
7.879 |
10.828 |
设椭圆
的左焦点为
，离心率为
，过点且与
轴垂直的直线被椭圆截得的线段长为
.
(1) 求椭圆方程.
(2) 过点
的直线
与椭圆交于不同的两点
，当
面积最大时，求
.
在一次数学考试中，第22,23,24题为选做题，规定每位考生必须且只须在其中选做一题，设5名考生选做这三题的任意一题的可能性均为
，每位学生对每题的选择是相互独立的，各学生的选择相互之间没有影响.
（1）求其中甲、乙两人选做同一题的概率；
（2）设选做第23题的人数为
，求的分布列及数学期望.
如图，四棱锥P-ABCD中，
，
，
，
，
是
的中点．
（1）求证：
；
（2）求二面角
的平面角的正弦值．
已知函数
.
(1)求
的单调递增区间；
(2)在
中，三内角
的对边分别为
，已知
,
,
.求
的值.
设函数
．
（1）当
时，求曲线
在
处的切线方程；
（2）当
时，求函数的单调区间；
（3）在（2）的条件下，设函数
，若对于
[1，2]，
[0，1]，使
成立，求实数
的取值范围．