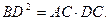(本小题14分)已知函数 ,
,
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)这直线 是曲线
是曲线 的切线,若
的切线,若 的斜率存在最小值
的斜率存在最小值 ,求
,求 的值,并求取得最小斜率时切线
的值,并求取得最小斜率时切线 的方程;
的方程;
(3)已知 分别在
分别在 处取得极值,求证:
处取得极值,求证: .
.
已知函数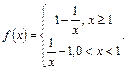
(1)当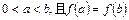 时,求
时,求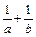 的值;
的值;
(2)是否存在实数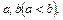 使
使 的定义域、值域都是
的定义域、值域都是
若存在,求出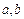 的值;若不存在,说明理由。
的值;若不存在,说明理由。
把一根长度为8的铁丝截成3段。
(1)若三段的长度均为整数,求三段的长度能构成三角形的概率;
(2)若把铁丝截成2,2,4的三段放入一盒子中,然后有放回地摸4次,设摸到长度为2的铁丝的次数为 求
求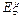 与
与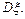
在直角坐标系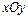 中,直线
中,直线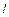 的参数方程为
的参数方程为
在极坐标系(与直角坐标系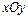 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为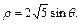
(1)求圆C的直角坐标方程;
(2)设圆C与直线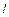 交于点A,B,若点P的坐标为
交于点A,B,若点P的坐标为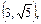 求
求
如图所示,圆 的直径
的直径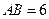 ,
, 为圆周上一点,
为圆周上一点,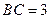 .过
.过 作圆的切线
作圆的切线 ,过
,过 作
作 的垂线
的垂线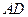 ,
,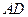 分别与直线
分别与直线 、圆交于点
、圆交于点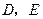 ,求
,求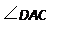 和线段
和线段 的长。
的长。
已知:如图,等腰 中,
中,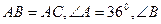 的平分线交
的平分线交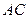 于D,求证:(1)BD=BC;
于D,求证:(1)BD=BC;
(2)