某市四所中学报名参加某高校今年自主招生的学生人数如下表所示：-优题课

题文

某市四所中学报名参加某高校今年自主招生的学生人数如下表所示：

中学
人数

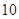为了了解参加考试的学生的学习状况，该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查．
（1）问四所中学各抽取多少名学生？
（2）从参加问卷调查的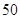名学生中随机抽取两名学生，求这两名学生来自同一所中学的概率；
（3）在参加问卷调查的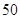名学生中，从来自两所中学的学生当中随机抽取两名学生，用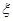表示抽得中学的学生人数，求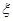的分布列．

科目数学题型解答题难度较易

知识点：随机抽样

登录免费查看答案和解析

相关试题

某市公租房的房源位于 $A, B, C$ 个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，求该市的4位申请人中：
（I）没有人申请 $A$ 片区房源的概率；
（II）每个片区的房源都有人申请的概率．

设 ${a_{n}}$ 是公比为正数的等比数列 $a_{1} = 2, a_{3} = a_{2} + 4$ ．
（Ⅰ）求 ${a_{n}}$ 的通项公式；
（Ⅱ）设 ${b_{n}}$ 是首项为1，公差为2的等差数列，求数列 ${a_{n} + b_{n}}$ 的前 $n$ 项和 $S_{n}$ ．

已知数列 $\{a_{n}\}$ 与 $\{b_{n}\}$ 满足 ${b_{n}}_{+ 1} a_{n} + b_{n} a_{n + 1} = {(- 2)}^{n} + 1, b_{n} = \frac{3 + {(- 1)}^{n - 1}}{2}, n \in N *, 且 a_{1} = 2 ．$

（1）求 $a_{2}, a_{3}$ 的值
（2）设 $c_{n} = a_{2 n + 1} ﹣ a_{2 n - 1}, n \in N^{*}$ ,证明 $\{c_{n}\}$ 是等比数列
（3）设 $S_{n}$ 为 $\{a_{n}\}$ 的前 $n$ 项和,证明 $\frac{S_{1}}{a_{1}} + \frac{S_{2}}{a_{2}} + \dots + \frac{S_{2 n - 1}}{a_{2 n - 1}} + \frac{S_{2 n}}{a_{2 n}} ⩽ n - \frac{1}{3} (n \in N^{*})$

已知函数 $f (x) = 4 x^{3} + 3 t x^{2} - 6 t^{2} x + t - 1$ ， $x \in R$ ，其中 $t \in R$ ．
（Ⅰ）当 $t = 1$ 时，求曲线 $y = f (x)$ 在点 $(0, f (0))$ 处的切线方程；
（Ⅱ）当 $t \neq 0$ 时，求 $f (x)$ 的单调区间；
（Ⅲ）证明：对任意的 $t \in (0, + \infty)$ ， $f (x)$ 在区间 $(0, 1)$ 内均存在零点．

设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}, F_{2}$ ,点 $P (a, b)$ 满足 $|P F_{2}| = |F_{1} F_{2}|$ ．
（1）求椭圆的离心率 $e$ ；

(2)设直线 $P F_{2}$ 与椭圆 ${(x + 1)}^{2} + {(y - \sqrt{3})}^{2} = 16$ 相交于 $A, B$ ,两点若直线 $P F_{2}$ 与圆相交于 $M, N$ 两点,且 $|M N| = \frac{5}{8} |A B|$ ,求椭圆的方程．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号