某市举行了“高速公路免费政策”满意度测评,共有1万人参加了这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
| 组别 |
分组 |
频数 |
频率 |
| 1 |
 |
60 |
0.12 |
| 2 |
 |
120 |
0.24 |
| 3 |
 |
180 |
0.36 |
| 4 |
 |
130 |
c |
| 5 |
 |
a |
0.02 |
| 合计 |
b |
1.00 |
(1)求出表中 的值;
的值;
(2)若分数在(含60分)的人对“高速公路免费政策”表示满意,现从全市参加了这次满意度测评的人中随机抽取一人,求此人满意的概率;
(3)请你估计全市的平均分数.
设函数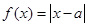 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若 的解集为
的解集为 ,
, ,求证:
,求证: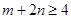 .
.
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线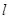 的极坐标方程为
的极坐标方程为 ,曲线C的参数方程是
,曲线C的参数方程是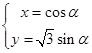 (
(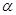 是参数).
是参数).
(1)求直线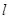 的直角坐标方程及曲线C的普通方程;
的直角坐标方程及曲线C的普通方程;
(2)求曲线C上的点到直线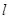 的最大距离.
的最大距离.
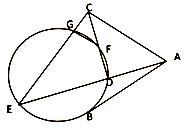
如图, 是
是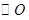 的一条切线,切点为B,ADE,CFD和CGE都是
的一条切线,切点为B,ADE,CFD和CGE都是 的割线,
的割线, .
.
(1)证明: ;
;
(2)证明:
已知函数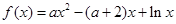 ,其中
,其中 .
.
(1)当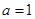 时,求曲线
时,求曲线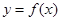 的点
的点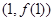 处的切线方程;
处的切线方程;
(2)当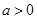 时,若
时,若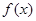 在区间
在区间 上的最小值为-2,求
上的最小值为-2,求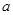 的取值范围;
的取值范围;
(3)若 ,且
,且 恒成立,求
恒成立,求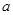 的取值范围.
的取值范围.