数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,则a8=( )
| A.0 | B.3 | C.8 | D.11 |
下列四组中的f(x),g(x),表示同一个函数的是()
| A.f(x)=1,g(x)=x0 |
B.f(x)=x﹣1,g(x)=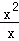 ﹣1 ﹣1 |
C.f(x)=x2,g(x)=(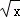 )4 )4 |
D.f(x)=x3,g(x)=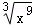 |
下列对象能构成集合的是()
| A.高一年级全体较胖的学生 |
| B.sin30°,sin45°,cos60°,1 |
| C.全体很大的自然数 |
| D.平面内到△ABC三个顶点距离相等的所有点 |
若定义在[﹣2013,2013]上的函数f(x)满足:对于任意的x1,x2∈[﹣2013,2013],有f(x1+x2)=f(x1)+f(x2)﹣2012,且x>0时,有f(x)>2012,f(x)的最大、小值分别为M、N,则M+N的值为()
| A.2011 | B.2012 | C.4022 | D.4024 |
下列四个说法:
(1)函数f(x)>0在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
(3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);
(4)y=1+x和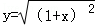 表示相等函数.
表示相等函数.
其中说法正确的个数是()
| A.0 | B.1 | C.2 | D.3 |
偶函数f(x)(x∈R)满足:f(﹣4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x3f(x)<0的解集为()
| A.(﹣∞,﹣4)∪(4,+∞) |
| B.(﹣4,﹣1)∪(1,4) |
| C.(﹣∞,﹣4)∪(﹣1,0) |
| D.(﹣∞,﹣4)∪(﹣1,0)∪(1,4) |