(本题满分为12分)
已知函数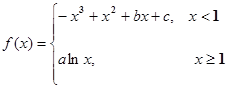 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点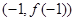 处的切线的斜率是
处的切线的斜率是 .
.
(1)求实数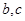 的值;
的值;
(2)求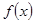 在区间
在区间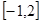 上的最大值;
上的最大值;
(3)对任意给定的正实数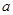 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得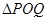 是以
是以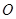 为直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
为直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
(本题满分为12分)
已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.
(I)求椭圆方程;
(II)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段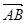 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
(本题满分为12分)
在四棱锥 中,
中,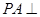 底面
底面 ,
, ,
,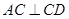 ,
,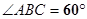 ,
,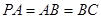 ,
, 是
是 的中点.
的中点.
(I)证明: ;
;
(II)证明: 平面
平面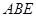 ;
;
(III)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
从全校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多?并求出该小组的频数,频率;
(4)估计这次竞赛中,成绩高于60分的学生占总人数的百分比.
(本小题满分12分)
已知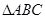 的面积
的面积 满足
满足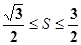 ,且
,且 ,
, 与
与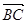 的夹角为
的夹角为 .
.
(1)求 的取值范围;
的取值范围;
(2)求函数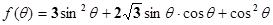 的最大值及最小值.
的最大值及最小值.