已知椭圆 与
与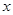 轴、
轴、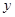 轴的正半轴分别交于
轴的正半轴分别交于 两点,原点
两点,原点 到直线
到直线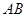 的距离为
的距离为 ,该椭圆的离心率为
,该椭圆的离心率为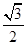 .
.
(1)求椭圆的方程;
(2)是否存在过点 的直线
的直线 与椭圆交于
与椭圆交于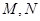 两个不同的点,使
两个不同的点,使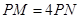 成立?若存在,求出
成立?若存在,求出 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x).
(1)求f(2 012)的值;
(2)求证:函数f(x)的图像关于直线x=2对称;
(3)若f(x)在区间[0,2]上是增函数,试比较f(-25),f(11),f(80)的大小.
已知函数f(x)=x2+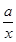 (x≠0,a∈R).
(x≠0,a∈R).
(1)判断函数f(x)的奇偶性;
(2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围.
已知二次函数f(x)满足条件f(0)=1,f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
设A,B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的只数多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为 ,服用B有效的概率为
,服用B有效的概率为 .
.
(1)求一个试验组为甲类组的概率;
(2)观察三个试验组,用X表示这三个试验组中甲类组的个数,求X的分布列和数学期望.
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品的检验费用为100元,且抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.