某次网球比赛分四个阶段，只有上一阶段的胜者，才能参加继续下一阶段的比赛，否则就被淘汰，选手每闯过一个阶段，个人积10分，否则积0分．甲、乙两个网球选手参加了此次比赛．已知甲每个阶段取胜的概率为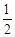
，乙每个阶段取胜的概率为
．
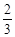（1）求甲、乙两人最后积分之和为20分的概率；
（2）设甲的最后积分为X，求X的分布列和数学期望.
（本小题12分）设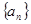
是一个公差为
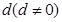的等差数列，它的前10项和
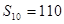且
，
，
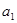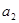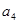成等比数列.（Ⅰ）证明
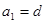；（Ⅱ）求公差
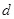的值和数列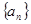的通项公式。
（本小题10分）△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60o，∠ADC＝150o，求AC的长及△ABC的面积．
（本小题满分12分）
如图，设矩形ABCD（AB>AD）的周长为24，把它关于AC折起来，AB折过去后，交DC于点P. 设AB="x," 求△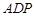
的最大面积及相应的x值.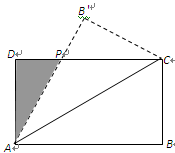
（本小题满分12分）
如图，在四边形ABCD中，AC平分∠DAB，∠ABC=600，AC=7，AD=6，S△ADC=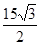
，
求AB的长.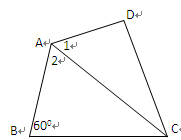
（本小题满分12分）
已知集合
，
求实数a的取值范围。