已知:一次函数 与
与 的图像的交点的坐标为P(1,–2).求:方程组
的图像的交点的坐标为P(1,–2).求:方程组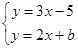 的解和b的值.
的解和b的值.
如图,已知在△ABC中,∠A = 90°, ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
(1)求PM的长;
(2)求y关于x的函数解析式,并写出它的定义域;
(3)联结MF、MG,当△PMF与△PMG相似时,求BM的长.
如图,在直角坐标系x O y中,二次函数 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图像上,且∠DAC = 45°,求点D的坐标.
已知:如图,在梯形ABCD中,AD // BC,AB⊥BC,点M在边BC上,且∠MDB =∠ADB, .
.
(1)求证:BM=CM;
(2)作BE⊥DM,垂足为点E,并交CD于点F.
求证: .
.
如图,在平行四边形ABCD中,点E在边BC上,联结AE并延长,交对角线BD于点F、DC的延长线于点G,如果 .
.
求 的值.
的值.
某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路的AB段为监测区(如图).在△ABP中,已知∠PAB = 32º,∠PBA = 45º,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?
(参考数据: ,
, ,
, ,
, )
)