(本题12分)已知圆心为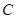 的圆经过点
的圆经过点 和
和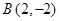 ,且圆心
,且圆心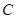 在直线
在直线 上
上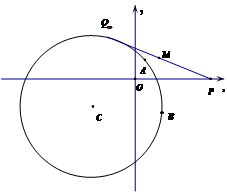
(1)求圆心为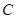 的圆的标准方程;
的圆的标准方程;
(2)线段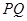 的端点
的端点 的坐标是
的坐标是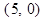 ,端点
,端点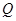 在圆
在圆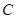 上运动,求线段
上运动,求线段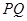 中点
中点 的轨迹方程.
的轨迹方程.
已知过点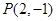 的直线
的直线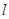 交椭圆
交椭圆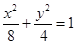 于
于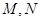 两点,
两点,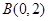 是椭圆的一个顶点,若线段
是椭圆的一个顶点,若线段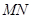 的中点恰为点
的中点恰为点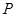 .
.
(1)求直线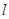 的方程;
的方程;
(2)求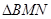 的面积.
的面积.
如图,菱形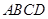 的边长为2,
的边长为2, 为正三角形,现将
为正三角形,现将 沿
沿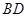 向上折起,折起后的点
向上折起,折起后的点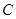 记为
记为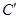 ,且
,且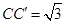 ,连接
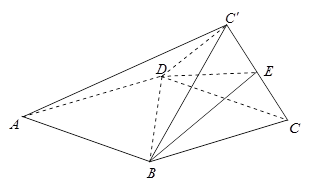
,连接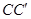 .
.
(1)若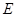 为
为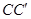 的中点,证明:
的中点,证明: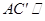 平面
平面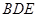 ;
;
(2)求三棱锥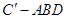 的体积.
的体积.
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
| 需求量(万吨) |
3 |
6 |
5 |
7 |
8 |
(1)利用所给数据求年需求量与年份之间的回归直线方程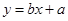 ;
;
(2)利用(1)中所求出的直线方程预测该地第6年的粮食需求量.
已知圆 的方程为
的方程为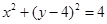 ,点
,点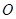 是坐标原点.直线
是坐标原点.直线 与圆
与圆 交于
交于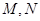 两点.
两点.
(1)求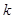 的取值范围;
的取值范围;
(2)过 作圆的弦,求最小弦长?
作圆的弦,求最小弦长?
已知条件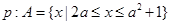 ,条件
,条件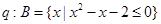 ,若
,若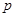 是
是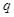 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.