如图，长为L的轻杆一端连着质量为m的小球，另一端用铰链固接于水平地面上的O点，初始时小球静止于地面上，边长为L、质量为M的正方体左侧静止于O点处。现在杆中点处施加一大小始终为12mg/π，方向始终垂直杆的力F，经过一段时间后撤去F，小球恰好能到达最高点。忽略一切摩擦，试求：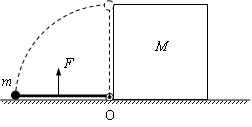
（1）力F所做的功；
（2）力F撤去时小球的速度；
（3）若小球运动到最高点后由静止开始向右倾倒，求杆与水平面夹角为θ时（正方体和小球还未脱离），正方体的速度大小。
如图所示，长12m质量为50kg的木板右端有一立柱．木板置于水平地面上，木板与地面间的动摩擦因数为0.1，质量为50kg的人立于木板左端，木板与人均静止，当人以4m/s2的加速度匀加速向右奔跑至板的右端时，立刻抱住立柱，(取g=10m/s2)试求：
(1)人在奔跑过程中受到的摩擦力的大小．
(2)人在奔跑过程中木板的加速度．
(3)人从开始奔跑至到达木板右端所经历的时间．
如图所示，AB是粗糙的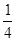
圆弧，半径为R，OA水平，OB竖直，O点离地面高度为2R，一质量为m的小球，从A点静止释放，不计空气阻力，最后落在距C点R处的D点。求：
（1）小球经过B点时，对轨道的压力大小。
（2）小球在AB段克服阻力做的功。
如图所示，质量为m的小球自由下落d后，沿竖直面内的固定轨道ABC运动，AB是半径为d的四分之一粗糙圆弧，BC是直径为d的光滑半圆弧，B是轨道的最低点，小球运动到C点对轨道的压力恰为零。求小球在AB圆弧上运动过程中，克服摩擦力做了多少功？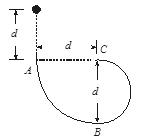
一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小。已知地球半径R=6400km，地球表面重力加速度g=10m/s2.
如图所示，飞行员的质量为m=60kg，重力加速度为g=10m/s2，他驾驶飞机在竖直平面内做翻筋斗的圆周运动，当飞机飞到最高点时速度为
，飞行员对机座的压力恰好为零，则轨道半径R=m，若飞机飞到最低点时速度为
，飞行员对机座的压力N=N。