已知函数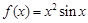 ,各项均不相等的有限项数列
,各项均不相等的有限项数列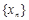 的各项
的各项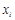 满足
满足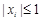 .令
.令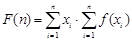 ,
,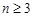 且
且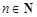 ,例如:
,例如: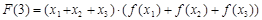 .
.
(Ⅰ)若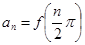 ,数列
,数列 的前n项和为Sn,求S19的值;
的前n项和为Sn,求S19的值;
(Ⅱ)试判断下列给出的三个命题的真假,并说明理由。
①存在数列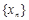 使得
使得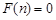 ;②如果数列
;②如果数列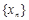 是等差数列,则
是等差数列,则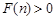 ;
;
③如果数列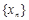 是等比数列,则
是等比数列,则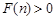 。
。
(本小题满分14分)已知数列{an}是等差数列,{bn}是等比数列,且满足a1+a2+a3=9,b1b2b3=27.若a4=b3,b4-b3=m.
(1)当m=18时,求数列{an}和{bn}的通项公式;
(2)若数列{bn}是唯一的,求m的值.
(本小题满分14分)如图,在四面体 中,
中, ,点
,点 是
是 的中点,点
的中点,点 在线段
在线段 上,且
上,且 .
.
(1)若 ∥平面
∥平面 ,求实数
,求实数 的值;
的值;
(2)求证:平面 平面
平面 .
.
(本小题满分14分)已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量 ,
, ,且
,且 .
.
(1)求角A的大小;
(2)若 ,求证:
,求证: 为等边三角形.
为等边三角形.
记数列{an}的前n项和为Sn,若不等式 对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为.
对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为.
(本小题满分16分)已知函数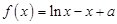 有且只有一个零点.
有且只有一个零点.
(1)求a的值;
(2)若对任意的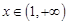 ,有
,有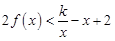 恒成立,求实数k的最小值;
恒成立,求实数k的最小值;
(3)设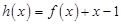 ,对任意
,对任意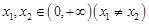 ,证明:不等式
,证明:不等式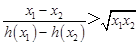 恒成立.
恒成立.