(本小题满分16分)已知函数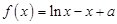 有且只有一个零点.
有且只有一个零点.
(1)求a的值;
(2)若对任意的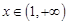 ,有
,有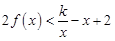 恒成立,求实数k的最小值;
恒成立,求实数k的最小值;
(3)设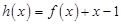 ,对任意
,对任意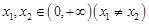 ,证明:不等式
,证明:不等式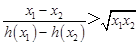 恒成立.
恒成立.
(本小题满分16分)在数列 ,
,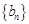 中,已知
中,已知 ,
,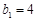 ,且
,且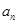 ,
, ,
, 成等差数列,
成等差数列, ,
,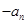 ,
, 也成等差数列.
也成等差数列.
(1)求证: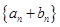 是等比数列;
是等比数列;
(2)设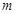 是不超过100的正整数,求使
是不超过100的正整数,求使 成立的所有数对
成立的所有数对 .
.
(本小题满分16分)已知函数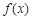 满足
满足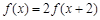 ,且当
,且当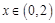 时,
时, ,当
,当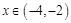 时,
时,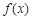 的最大值为
的最大值为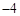 .
.
(1)求实数a的值;
(2)设 ,函数
,函数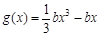 ,
,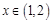 .若对任意
.若对任意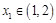 ,总存在
,总存在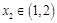 ,使
,使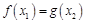 ,求实数b的取值范围.
,求实数b的取值范围.
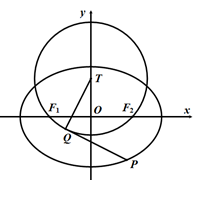
(本小题满分16分)如图,在平面直角坐标系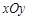 中,椭圆
中,椭圆 的左,右顶点分别为
的左,右顶点分别为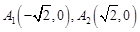 ,若直线
,若直线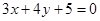 上有且仅有一个点
上有且仅有一个点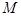 ,使得
,使得 .
.
(1)求椭圆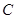 的标准方程;
的标准方程;
(2)设圆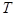 的圆心
的圆心 在x轴上方,且圆
在x轴上方,且圆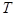 经过椭圆
经过椭圆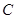 两焦点.点
两焦点.点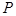 ,
,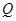 分别为椭圆
分别为椭圆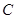 和圆
和圆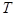 上的一动点.若
上的一动点.若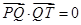 时,
时, 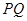 取得最大值为
取得最大值为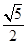 ,求实数
,求实数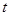 的值.
的值.
(本小题满分14分)如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD.设 .
.
(1)现要在景区内铺设一条观光道路,由线段AB、BC、CD和DA组成,则当θ为何值时,观光道路的总长l最长,并求l的最大值.
(2)若要在景区内种植鲜花,其中在 和
和 内种满鲜花,
内种满鲜花,
在扇形 内种一半面积的鲜花,则当θ为何值时,鲜花种植面积S最大.
内种一半面积的鲜花,则当θ为何值时,鲜花种植面积S最大.
如图,边长为2的正方形 是圆柱的中截面,点
是圆柱的中截面,点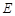 为线段
为线段 的中点,点
的中点,点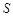 为圆柱的下底面圆周上异于
为圆柱的下底面圆周上异于 ,
,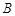 的一个动点.
的一个动点.
(1)在圆柱的下底面上确定一定点 ,使得
,使得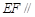 平面
平面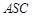 ;
;
(2)求证:平面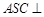 平面
平面 .
.