已知椭圆的两个焦点为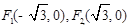 ,离心率
,离心率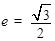 .
.
(1)求椭圆的方程;
(2)设直线 ,若
,若 与椭圆交于
与椭圆交于 两点,且
两点,且 等于椭圆的短轴长,求
等于椭圆的短轴长,求 的值;
的值;
(3)若直线 ,若
,若 与椭圆交于两个不同的点A和B,且使
与椭圆交于两个不同的点A和B,且使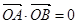 ,问这样的直线存在吗?若存在求
,问这样的直线存在吗?若存在求 的值,若不存在说明理由。
的值,若不存在说明理由。
B在A地的正东400千米处.
(1) 台风移动路径所在的直线方程;
(2)求城市B处于危险区内的时间是多少小时?

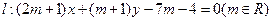
(1)证明:不论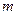 为何值时,直线和圆恒相交于两点;
为何值时,直线和圆恒相交于两点;
(2)求直线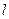 被圆
被圆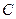 截得的弦长最小时的方程.
截得的弦长最小时的方程.

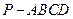
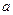
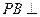 平面
平面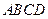 ,M、N分别是AB、PC的中点。
,M、N分别是AB、PC的中点。
(1)求证:MN//平面PAB;
(2)若平面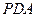 与平面
与平面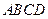 成
成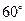 的二面角,
的二面角,
求该四棱锥的体积.
在 中,
中, ,
, .
.
(1)求角 的大小;
的大小;
(2)若 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
调查某市出租车使用年限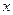 和该年支出维修费用
和该年支出维修费用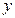 (万元),得到数据如下:
(万元),得到数据如下:
使用年限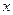 |
2 |
3 |
4 |
5 |
6 |
维修费用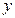 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.(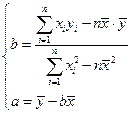 )
)