(本小题满分13分)已知定义在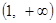 上的函数
上的函数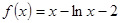 ,
,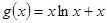 .
.
(1)求证: 存在唯一的零点,且零点属于(3,4);
存在唯一的零点,且零点属于(3,4);
(2)若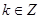 且
且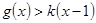 对任意的
对任意的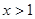 恒成立,求
恒成立,求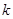 的最大值.
的最大值.
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间
与时间 小时
小时 间的关系为
间的关系为 .如果在前
.如果在前 个小时消除了
个小时消除了 的污染物,试求:
的污染物,试求:
(1) 个小时后还剩百分之几的污染物?
个小时后还剩百分之几的污染物?
(2)污染物减少 所需要的时间.(参考数据:
所需要的时间.(参考数据: )
)
已知函数 。
。
(1)求函数 的单调递减区间;
的单调递减区间;
(2)求函数 在区间
在区间 上的最大值及最小值;
上的最大值及最小值;
(3)将函数 的图象作怎样的变换可得到
的图象作怎样的变换可得到 的图象?
的图象?
已知平面直角坐标系内三点 、
、 、
、 在一条直线上,
在一条直线上, ,
, ,
, ,且
,且 ,其中
,其中 为坐标原点.
为坐标原点.
(1)求实数 ,
, 的值;
的值;
(2)设 的重心为
的重心为 ,若存在实数
,若存在实数 ,使
,使 ,试求
,试求 的大小.
的大小.
对于函数 (
( ).
).
(1)探索并证明函数 的单调性;
的单调性;
(2)是否存在实数 使函数
使函数 为奇函数?若有,求出实数
为奇函数?若有,求出实数 的值,并证明你的结论;若没有,说明理由.
的值,并证明你的结论;若没有,说明理由.
设全集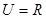 ,集合
,集合 为第二象限角
为第二象限角 ,集合
,集合 为第四象限角
为第四象限角 .
.
(1)分别用区间表示集合 与集合
与集合 ;(2)分别求
;(2)分别求 和
和 .
.