(本小题满分10分)选修4-1:几何证明选讲
已知△ABC中, ,D为△ABC 外接圆劣弧AC上的点(不与点A、C重合),延长BD至E,延长AD交BC的延长线于F.
,D为△ABC 外接圆劣弧AC上的点(不与点A、C重合),延长BD至E,延长AD交BC的延长线于F.
(Ⅰ)求证: ;
;
(Ⅱ)求证: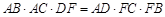 .
.
(本小题满分13分)
某设计部门承接一产品包装盒的设计(如图所示),客户除了要求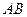 、
、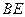 边的长分别为
边的长分别为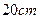 和
和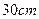 外,还特别要求包装盒必需满足:①平面
外,还特别要求包装盒必需满足:①平面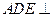 平面
平面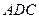 ;②平面
;②平面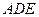 与平面
与平面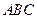 所成的二面角不小于
所成的二面角不小于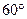 ;③包装盒的体积尽可能大。
;③包装盒的体积尽可能大。
若设计部门设计出的样品满足: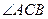 与
与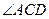 均为直角且
均为直角且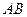 长
长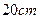 ,矩形
,矩形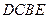 的一边长为
的一边长为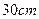 ,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
,请你判断该包装盒的设计是否能符合客户的要求?说明理由.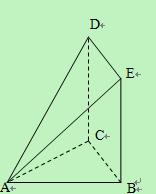
(本小题满分13分)
某慈善机构举办一次募捐演出,有一万人参加,每人一张门票,每张100元. 在演出过程中穿插抽奖活动.第一轮抽奖从这一万张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数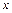 ,
,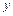 (
(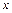 ,
,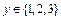 ),随即按如右所示程序框图运行相应程序.若电脑显示“中奖”,则抽奖者获得9000元奖金;若电脑显示“谢谢”,则不中奖.
),随即按如右所示程序框图运行相应程序.若电脑显示“中奖”,则抽奖者获得9000元奖金;若电脑显示“谢谢”,则不中奖.
(Ⅰ)已知小曹在第一轮抽奖中被抽中,求小曹在第二轮抽奖中获奖的概率;
(Ⅱ)若小叶参加了此次活动,求小叶参加此次活动收益的期望;
(Ⅲ)若此次募捐除奖品和奖金外,不计其它支出,该机构想获得96万元的慈善款.问该慈善机构此次募捐是否能达到预期目标.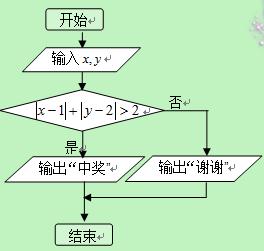
(本小题满分13分)
已知圆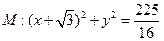 的圆心为
的圆心为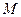 ,圆
,圆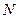 :
: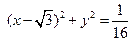 的圆心为
的圆心为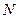 ,一动圆与圆
,一动圆与圆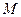 内切,与圆
内切,与圆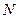 外切.
外切.
(Ⅰ)求动圆圆心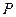 的轨迹方程;
的轨迹方程;
(Ⅱ)在(Ⅰ)所求轨迹上是否存在一点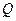 ,使得
,使得 为钝角?若存在,求出点
为钝角?若存在,求出点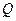 横坐标的取值范围;若不存在,说明理由.
横坐标的取值范围;若不存在,说明理由.
(本小题满分13分)
在锐角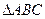 中,
中,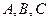 三内角所对的边分别为
三内角所对的边分别为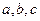 .
.
设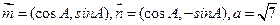 ,
,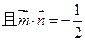
(Ⅰ)若 ,求
,求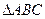 的面积;
的面积;
(Ⅱ)求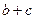 的最大值.
的最大值.
(本小题满分12分)
若实数列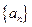 满足
满足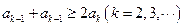 ,则称数列
,则称数列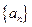 为凸数列.
为凸数列.
(Ⅰ)判断数列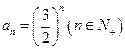 是否是凸数列?
是否是凸数列?
(Ⅱ)若数列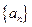 为凸数列,
为凸数列, 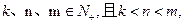
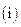 求证:
求证: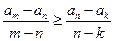 ;
;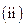 设
设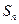 是数列
是数列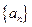 的前
的前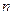 项和,求证:
项和,求证: .
.