如图，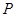
为某湖中观光岛屿，
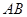是沿湖岸南北方向道路，
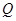为停车场，
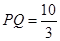
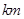，某旅游团浏览完岛屿后，乘游船回停车场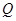，已知游船以
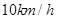的速度沿方位角
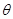的
方向行驶，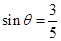
．游船离开观光岛屿
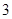分钟后，因事耽搁没有来得及登上游船的游客甲，为了及时
赶到停车地点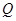与旅游团会合，立即决定租用小艇先到达湖岸南北大道
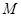处，然后乘景区电动出租车到
停车场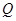处（假设游客甲到达湖滨大道后幸运地一点未耽搁便乘上了电动出租车）．游客甲乘小艇行驶的
方位角是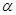
，电动出租车的速度为
．
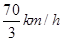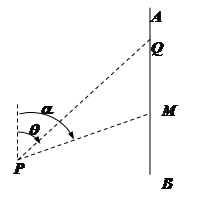
（Ⅰ）设
，问小艇的速度为多少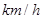
时，游客甲才能与游船同时到达点；
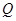（Ⅱ）设小艇速度为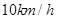，请你替该游客设计小艇行驶的方位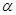角，当角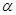的余弦值是多少时，游客甲能按计划以最短时间到达．
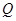的方程
有实根.
的值;
的所有根均为整数，求整数
的值.
中，AB是⊙O的直径，⊙O与AC交于点D，
，求
的度数；
，
取何值时，
随