如图，
为某湖中观光岛屿，
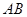是沿湖岸南北方向道路，
为停车场，
，某旅游团浏览完岛屿后，乘游船回停车场，已知游船以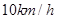
的速度沿方位角
的
方向行驶，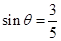
．游船离开观光岛屿
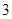分钟后，因事耽搁没有来得及登上游船的游客甲，为了及时
赶到停车地点与旅游团会合，立即决定租用小艇先到达湖岸南北大道
处，然后乘景区电动出租车到
停车场处（假设游客甲到达湖滨大道后幸运地一点未耽搁便乘上了电动出租车）．游客甲乘小艇行驶的
方位角是
，电动出租车的速度为
．
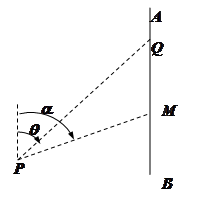
（Ⅰ）设
，问小艇的速度为多少
时，游客甲才能与游船同时到达点；
（Ⅱ）设小艇速度为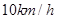，请你替该游客设计小艇行驶的方位角，当角的余弦值是多少时，游客甲能按计划以最短时间到达．
如图，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB，BP＝BC＝2，E，F分别是PB，PC的中点。
（1）证明：EF∥平面PAD；
（2）求三棱锥E－ABC的体积V。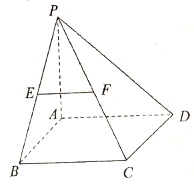
已知Rt△ABC的顶点坐标A（-3，0），直角顶点B（-1，-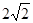
），顶点C在
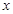轴上。
（1）求BC边所在直线的方程；
（2）圆M为Rt△ABC外接圆，其中M为圆心，求圆M的方程；
（3）直线
与Rt△ABC外接圆相切于第一象限，求切线与两坐标轴所围成的三角形面积最小时的切线方程。
已知O为坐标原点，△AOB中，边OA所在的直线方程是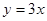
，边AB所在的直线方程是
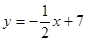，且顶点B的横坐标为6。
（1）求△AOB中，与边AB平行的中位线所在直线的方程；
（2）求△AOB的面积；
（3）已知OB上有点D，满足△AOD与△ABD的面积比为2，求AD所在的直线方程。
定义：如果数列
的任意连续三项均能构成一个三角形的三边长，则称为“三角形”数列．对于“三角形”数
列，如果函数
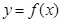使得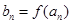
仍为一个“三角形”数列，则称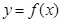是数列的“保三角形函数”，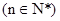
.
（Ⅰ）已知
是首项为2，公差为1的等差数列，若
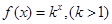是数列的“保三角形函数”，求k的取值范围；
（Ⅱ）已知数列
的首项为2010，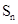
是数列的前n项和，且满足
，证明是“三角形”数列；
（Ⅲ）根据“保三角形函数”的定义，对函数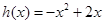
，
，和数列1，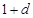
，
，（
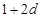）提出一个正确的命题，并说明理由．
设数列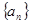
中，若
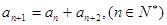，则称数列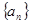为“凸数列”．
（Ⅰ）设数列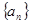为“凸数列”，若
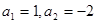，试写出该数列的前6项，并求出该6项之和；
（Ⅱ）在“凸数列”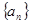中，求证：
；
（Ⅲ）设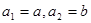
，若数列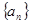为“凸数列”，求数列前
项和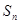
．