(本题10分)如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD, 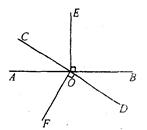
(1)图中与∠COE互余的角是_______ _______;图中与∠COE互补的角是_________ _____;(把符合条件的角都写出来)
(2)如果∠AOC=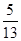 ∠EOF,求∠AOC的度数.
∠EOF,求∠AOC的度数.
如图,直线y=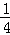 x与双曲线y=
x与双曲线y=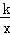 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).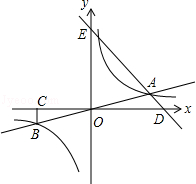
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数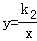 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.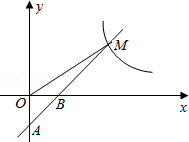
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
如图,一次函数y=kx+b的图象与反比例函数y=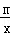 的图象相交于点A(﹣1,2)、点B(﹣4,n)
的图象相交于点A(﹣1,2)、点B(﹣4,n)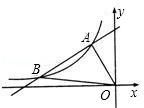
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
已知双曲线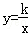 与直线
与直线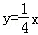 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线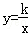 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线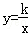 于点E,交BD于点C.
于点E,交BD于点C.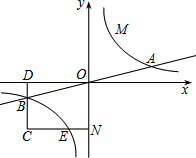
(1)若点D坐标是(﹣8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
已知,如图,正比例函数y=ax的图象与反比例函数y=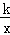 的图象交于点A(3,2)
的图象交于点A(3,2)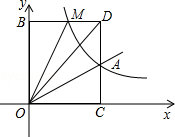
(1)填空:a= ;k= .
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
①当BM=DM时,求△ODM的面积;
②当BM=2DM时,求出直线MA的解析式.