一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
| |
平均分 |
方差 |
中位数 |
合格率 |
优秀率 |
| 甲组 |
6.9 |
2.4 |
|
91.7% |
16.7% |
| 乙组 |
|
1.3 |
|
83.3% |
8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.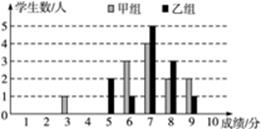
某海滨浴场的海岸线可以看作直线l(如图),有两位救生员在岸边的点A同时接到了海中的点B(该点视为定点)的呼救信号后,立即从不同的路径前往救助。其中1号救生员从点A先跑300米到离点B最近的点D,再跳入海中沿直线游到点B救助;2号救生员先从点A跑到点C,再跳入海中沿直线游到点B救助。如果两位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,且∠BAD=450,∠BCD=600,请问1号救生员与2号救生员谁先到达点B?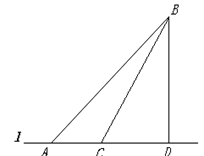
如图,在平面直角坐标系中,四边形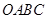 为矩形,
为矩形,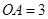 ,
,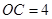 ,
,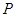 为直线
为直线 上一动点,将直线
上一动点,将直线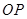 绕点
绕点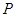 逆时针方向旋转
逆时针方向旋转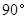 交直线
交直线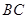 于点
于点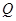 ;
;
当点
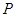 在线段
在线段 上运动(不与
上运动(不与 重合)时,
重合)时,
求证:OA·BQ=AP·BP;在(1)成立的条件下,设点
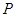 的横坐标为
的横坐标为 ,
,
线段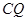 的长度为
的长度为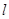 ,求出
,求出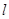 关于
关于 的函数解析式,
的函数解析式,
并判断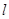 是否存在最小值,若存在,请求出最小值;
是否存在最小值,若存在,请求出最小值;
若不存在,请说明理由。直线
 上是否存在点
上是否存在点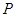 ,使
,使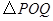 为等腰三角形,若存在,
为等腰三角形,若存在,
请求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每 台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.今年三月份甲种电脑
 每台售价多少元?
每台售价多少元?为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
如果乙种电脑每台售价为3800元,为打开乙种电脑的销路
 ,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少?
,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少?
有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开
(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).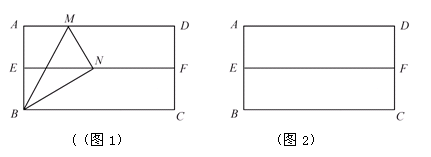
请解答以下问题:如图2,若延长MN交线段BC于P,△BMP是什么三角形?请证明你的结论.
在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP
如图,过点P(2,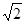 )作
)作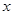 轴的平行线交
轴的平行线交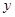 轴于点
轴于点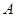 ,交双曲线
,交双曲线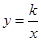 (
(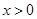 )于点
)于点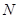 ,作
,作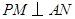 交双曲线
交双曲线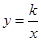 (
(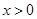 )于点
)于点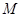 ,连结
,连结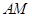 .已 知
.已 知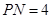
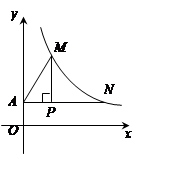
求
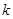 的值
的值设直线MN解析式为
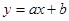 ,
,
求不等式 ≥
≥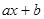 的解集;
的解集;