如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过网格点A（0，4）、B（-4，4）、C（-6，2），请在网格图中进行如下操作：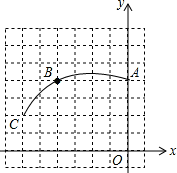
（1）利用网格图确定该圆弧所在圆心D点的位置（保留画图痕迹），则写出D点坐标为 ；
（2）连结AD，CD，求⊙D的半径长为 （结果保留根号），∠ADC的度数为 ；
（3）求扇形DAC是一个圆锥的侧面展开图，求该圆锥的底面半径长．（结果保留根号）
如图，
是⊙O的直径，
为延长线上的一点，
交⊙O于点
，且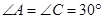
．
（1）求证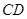：是⊙O的切线；
（2）请直接写出图中某３条线段之间的等量关系式，只要写出3个。（添加的辅助线不能用）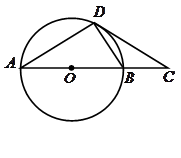
解方程：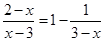 
计算: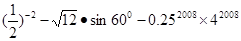 
已知二次函数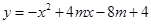
：
(1) 证明：当m为整数时，抛物线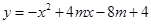与x轴交点的横坐标均为整数；
(2) 以抛物线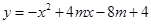的顶点A为等腰Rt△的直角顶点，作该抛物线的内接等腰Rt△ABC（B、C两点在抛物线上），求Rt△ABC的面积（图中给出的是m取某一值时的示意图）；
(3) 若抛物线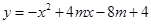与直线y＝7交点的横坐标均为整数，求整数m的值.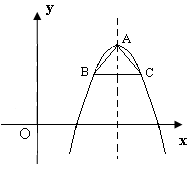
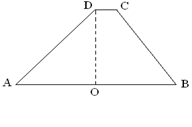
如图，已知梯形ABCD的下底边长AB＝8cm，上底边长DC＝1cm，O为AB的中点，梯形的高DO＝4cm. 动点P自A点出发，在AB上匀速运行，动点Q自点B出发，沿B→C→D→A匀速运行，速度均为每秒1个单位，当其中一个动点到达终点时，另一动点也同时停止运动. 设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）.
（1）求S随t变化的函数关系式及t的取值范围；
（2）当t为何值时S的值最大？说明理由.