(原创)某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示,光滑轨道中间部分水平,右侧为位于竖直平面内半径为R的半圆,在最低点与直轨道相切.5个大小相同、质量不等的小球并列静置于水平部分,球间有微小间隔,从左到右,球的编号依次为0、1、2、3、4,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将0号球向左拉至左侧轨道距水平高h处,然后由静止释放,使其与1号球碰撞,1号球再与2号球碰撞……所有碰撞皆为无机械能损失的正碰(不计空气阻力,小球可视为质点,重力加速度为g).
(1)0号球与1号球碰撞后,1号球的速度大小v1;
(2)若已知h=0.1m,R=0.64m,要使4号球碰撞后能过右侧轨道的最高点,问k值为多少?
一辆汽车从A点由静止出发做匀加速直线运动,用t=" 4" s的时间通过一座长x=" 24" m的平桥BC,过桥后的速度是vc=" 9" m/ s.求:
(1)它刚开上桥头时的速度vB有多大?
(2)桥头与出发点相距多远?
如图所示,一个质量为m,电荷量+q的带电微粒(重力忽略不计),从静止开始经U1电压加速后,水平进入两平行金属板间的偏转电场中,金属板长L,两板间距d,微粒射出偏转电场时的偏转角θ=30°,又接着进入一个方向垂直于纸面向里的匀强磁场区,求: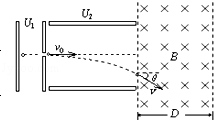
(1)微粒进入偏转电场时的速度v0是多大?
(2)两金属板间的电压U2是多大?
(3)若该匀强磁场的磁感应强度B,微粒在磁场中运动后能从左边界射出,则微粒在磁场中的运动时间为多少?
(4)若该匀强磁场的宽度为D,为使微粒不会从磁场右边射出,该匀强磁场的磁感应强度B至少多大?
如图所示,半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置,末端N与一长L=0.8m的水平传送带相切,水平衔接部分摩擦不计,传动轮(轮半径很小)作顺时针转动,带动传送带以恒定的速度ν0运动.传送带离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离S=1m,B点在洞口的最右端.现使质量为m=0.5kg的小物块从M点由静止开始释放,经过传送带后做平抛运动,最终落入洞中,传送带与小物块之间的动摩擦因数μ=0.5. g取10m/s2.求: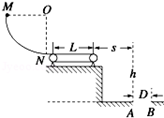
(1)小物块到达圆轨道末端N时对轨道的压力
(2)若ν0=3m/s,求物块在传送带上运动的时间
(3)若要使小物块能落入洞中,求ν0应满足的条件.
如图所示,足够长的光滑金属导轨与水平面的夹角为θ,两导轨间距为L,在导轨上端接入电源和滑动变阻器,电源电动势为E,内阻为r.一质量为m的导体棒ab与两导轨垂直并接触良好,整个装置处于磁感应强度为B,垂直于斜面向上的匀强磁场中,导轨与导体棒的电阻不计.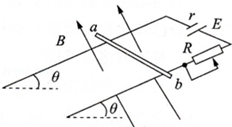
(1)若要使导体棒ab静止于导轨上,求滑动变阻器的阻值应取何值;
(2)若将滑动变阻器的阻值取为零,由静止释放导体棒ab,求释放瞬间导体棒ab的加速度;
(3)求第(2)问所示情况中导体棒ab所能达到的最大速度的大小.
传送带以恒定速度v=4 m/s顺时针运行,传送带与水平面的夹角θ=37°.现将质量m=2 kg的小物品轻放在其底端(小物品可看成质点),平台上的人通过一根轻绳用恒力F=20 N拉小物品,经过一段时间物品被拉到离地高为H=1.8 m的平台上,如图所示.已知物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,g取10 m/s2,已知sin37°=0.6,cos37°=0.8.求: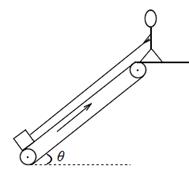
(1)物品从传送带底端运动到平台上所用的时间是多少?
(2)若在物品与传送带达到同速瞬间撤去恒力F,则物品还需多少时间才能离开皮带?