(本小题满分14分)已知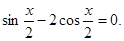
(1)求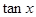 的值;
的值;
(2)求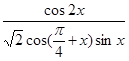 的值。
的值。
已知曲线C的极坐标方程是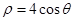 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是 (t是参数).
(t是参数).
(1)将曲线C的极坐标方程和直线L参数方程转化为普通方程;
(2)若直线L与曲线C相交于M、N两点,且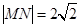 ,求实数m的值.
,求实数m的值.
如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P.
(1)求证: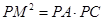 ;
;
(2)若⊙O的半径为 ,OA=
,OA= OM,求MN的长.
OM,求MN的长.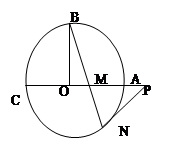
设函数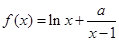 在
在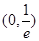 内有极值.
内有极值.
(1)求实数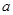 的取值范围;
的取值范围;
(2)若 求证:
求证: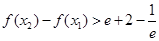 .
.
设椭圆C: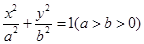 的离心率
的离心率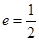 ,右焦点到直线
,右焦点到直线 1的距离
1的距离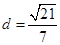 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A、B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| 有关系 |
无关系 |
不知道 |
|
| 40岁以下 |
800 |
450 |
200 |
| 40岁以上(含40岁) |
100 |
150 |
300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从持有关系态度的人中抽取45人,求n的值.
(2)在持“不知道”态度的人中,用分层抽样的方法抽取10人看作一个总体.①从这10人中选取3人,求至少一人在40岁以下的概率;②从这10人中人选取3人,若设40岁以下的人数为X,求X的分布列和数学期望.