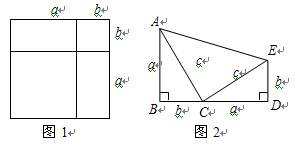
用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形和侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角不再利用).A方法:剪6个侧面;B方法:剪4个侧面和5个底面.现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面各数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
如图,已知直线 与
与 轴、
轴、 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线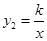 (
( <0)分别交于点C、D,且C点的坐标为(
<0)分别交于点C、D,且C点的坐标为( ,2).
,2).分别求出直线AB及双曲线的解析式;
求出点D的坐标;
利用图象直接写出:当x在什么范围内取值时,
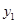 >
> .
.
 两地相距45千米,图中折线表示某骑车人离
两地相距45千米,图中折线表示某骑车人离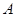 地的距离
地的距离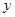 与时间
与时间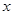 的函数关系.有一辆客车9点从
的函数关系.有一辆客车9点从 地出发,以45千米/时的速度匀速行驶,并往返于
地出发,以45千米/时的速度匀速行驶,并往返于 两地之间.(乘客上、下车停留时间忽略不计)
两地之间.(乘客上、下车停留时间忽略不计) 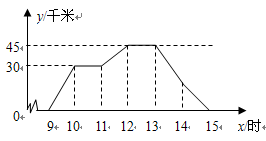
(1)从折线图可以看出,骑车人一共休息次,共休息小时;
(2)请在图中画出9点至15点之间客车与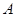 地距离
地距离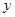 随时间
随时间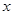 变化的函数图象;
变化的函数图象;
(3)通过计算说明,何时骑车人与客车第二次相遇.
某电信公司给顾客提供了两种手机上网计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间共有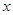 分钟,上网费用为
分钟,上网费用为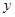 元.
元.
(1)分别写出顾客甲按A、B两种方式计费的上网费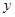 元与上网时间
元与上网时间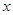 分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;
分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;
(2)如何选择计费方式能使上网费更合算?
(1)某居民小区搞绿化,要在一块长方形空地上建花坛,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个长方形场地成轴对称图形,你有好的设计方案吗?请在图22-1的长方形中画出你的设计方案;
(2)如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站A,使得货运站到三条公路的路程一样长,请在图22-2中画出,并标出货运站A的位置;
(1)如图1是一个重要公式的几何解释.请你写出这个公式;
(2)如图2, ,
,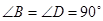 ,且
,且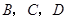 三点共线.
三点共线.
试证明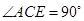 ;
;