17．已知甲同学手中藏有三张分别标有数字
，
，
的卡片，乙同学手中藏有三张分别标有数字，
，
的卡片，卡片外形相同．现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为
，
．
（1）请你用树形图或列表法列出所有可能的结果．
（2）现制定这样一个游戏规则：若所选出的，能使得
有两个不相等的实数根，则甲获胜；否则乙获胜．请问这样的游戏规则公平吗？请你用概率知识解释．
如图（1），直线y=k1 x+b与反比例函数y=
的图象交于点A（1，6），B（a，3）两点．
（1）求k1、k2的值；
（2）如图（1），等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点F，当梯形OBCD的面积为12时，请判断FC和EF的大小，并说明理由；
（3）如图（2），已知点Q是CD的中点，在第（2）问的条件下，点P在x轴上，从原点O出发，沿x轴负方向运动，设四边形PCQE的面积为S1，△DEQ的面积为S2，当∠PCD=90°时，求P点坐标及S1：S2的值．
已知，如图，PA是⊙O切线，切点为A，PB交⊙O于C且过圆心O，D是OB中点，连结AB并延长交⊙O于E，若∠APB=30°，AP=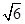
，求AE的长．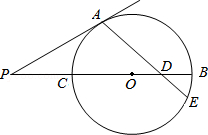
已知点M，N的坐标分别为（0，1），（0，-1），点P是抛物线y=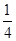
x2上的一个动点．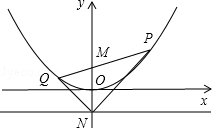
（1）求证：以点P为圆心，PM为半径的圆与直线y=-1的相切；
（2）设直线PM与抛物线y=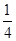x2的另一个交点为点Q，连接NP，NQ，求证：∠PNM=∠QNM．
如图，梯形ABCD中，AD∥BC，AB=DC，AE⊥BC于点E，AB的垂直平分线GF交BC于点F，交AB于点G，连接AF．已知AD=1．4，AF=5，GF=4．
（1）求梯形ABCD的腰AB的长；
（2）求梯形AFCD的面积．
计算题
（1）先化简，再求值：
，其中a=sin45°，b=cos30°；
（2）若关于x的方程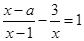
无解，求a的值．