如图（1），直线y=k1 x+b与反比例函数y=
的图象交于点A（1，6），B（a，3）两点．
（1）求k1、k2的值；
（2）如图（1），等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点F，当梯形OBCD的面积为12时，请判断FC和EF的大小，并说明理由；
（3）如图（2），已知点Q是CD的中点，在第（2）问的条件下，点P在x轴上，从原点O出发，沿x轴负方向运动，设四边形PCQE的面积为S1，△DEQ的面积为S2，当∠PCD=90°时，求P点坐标及S1：S2的值．
化简求值：已知
，求代数式
的值.
将以下有理数：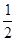
，|-2.5|，0，-22，-（+2），表示在数轴上，并用“<”将它们连接起来.
将
，
，
，
，
，
，
按要求分别填入相应的集合中.
（1）负数集合： ｛……｝;
（2）非负数集合：｛……｝;
（3）有理数集合：｛……｝
如图（1），将两块直角三角尺的直角顶点C叠放在一起，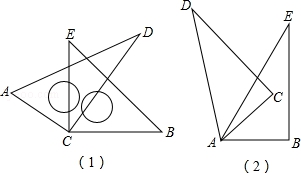
（1）若∠DCE=25°，∠ACB=；若∠ACB=150°，则∠DCE=；
（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；
（3）如图（2），若是两个同样的直角三角尺60°锐角的顶点A重合在一起，则∠DAB与∠CAE的大小又有何关系，请说明理由．
“水是生命之源”，某城市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：用水量/月 单价（元/m3）
| 不超过40m3 |
1 |
| 超过40m3的部分 |
1．5 |
另：每立方米用水加收0．2元的城市污水处理费
（1）如果1月份该用户用水量为34m3，那么该用户1月份应该缴纳水费元
（2）某用户2月份共缴纳水费65元，那么该用户2月份用水多少m3？
（3）若该用户水表3月份出了故障，只有70%的用水量记入水表中，这样该用户在3月份只缴纳了63．3元水费，问该用户3月份实际应该缴纳水费多少元？